MHB Amanda's question at Yahoo Answers regarding a solid of revolution

[MarkFL]

Here is the question:

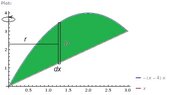
Calculus homework help?

Using the cylindrical shells method of integral calculus...what is the the volume bounded between y=4x-x^2 and y=x after a rotation across the y axis? Thank you!

Here is a link to the question:

Calculus homework help? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello amanda,

The first thing I like to do is create a sketch of the region to be revolved:

https://www.physicsforums.com/attachments/855._xfImport

Now, let's first determine the limits of integration by equating the two curves:

$$4x-x^2=x$$

Write in standard quadratic form:

$$x^2-3x=0$$

Factor:

$$x(x-3)=0$$

Hence $$x=0,\,3$$.

Now, the volume of an arbitrary shell is:

$$dV=2\pi rh\,dx$$ where

$$r=x$$

$$h=4x-x^2-x=3x-x^2$$

and so we have:

$$dV=2\pi x\left(3x-x^2 \right)\,dx=2\pi\left(3x^2-x^3 \right)\,dx$$

Now, summing the shells, we find:

$$V=2\pi\int_0^3 3x^2-x^3\,dx$$

Applying the anti-derivative form of the fundamental theorem of calculus, there results:

$$V=2\pi\left[x^3-\frac{1}{4}x^4 \right]_0^3=2\pi\left(3^3-\frac{3^4}{4} \right)=54\pi\left(1-\frac{3}{4} \right)=\frac{27\pi}{2}$$

I like to check my work by using another technique, and in this case we may use the washer method. This will mean setting up two integrals, one in which the line is the outer radius, and another in which the right side of the parabola is the outer radius. The left side of the parabola is the inner radius in both cases. We will need to solve the parabola for $x$. Writing it in vertex form, we have:

$$y=-(x-2)^2+4$$

$$(x-2)^2=4-y$$

$$x-2=\pm\sqrt{4-y}$$

$$x=2\pm\sqrt{4-y}$$

Interval 1: $$0\le y\le3$$

The volume of an arbitrary washer is

$$dV_1=\pi(R^2-r^2)\,dy$$ where:

$$R=y$$

$$r=2-\sqrt{4-y}$$

and so we have:

$$dV_1=\pi\left(y^2+y+4\sqrt{4-y}-8 \right)\,dy$$

Summing by integration:

$$V_1=\pi\int_0^3 y^2+y+4\sqrt{4-y}-8\,dy$$

Applying the anti-derivative form of the fundamental theorem of calculus, there results:

$$V_1=\pi\left[\frac{1}{3}y^3+\frac{1}{2}y^2-\frac{8}{3}(4-y)^{\frac{3}{2}}-8y \right]_0^3=\pi\left(\left(9+\frac{9}{2}-\frac{8}{3}-24 \right)-\left(-\frac{64}{3} \right) \right)=\frac{49\pi}{6}$$

Interval 2: $$3\le y\le4$$

The volume of an arbitrary washer is

$$dV_2=\pi(R^2-r^2)\,dy$$ where:

$$R=2+\sqrt{4-y}$$

$$r=2-\sqrt{4-y}$$

and so we have:

$$dV_2=8\pi\sqrt{4-y}\,dy$$

Summing by integration:

$$V_2=8\pi\int_3^4\sqrt{4-y}\,dy$$

Applying the anti-derivative form of the fundamental theorem of calculus, there results:

$$V_2=-\frac{16\pi}{3}\left[(4-y)^{\frac{3}{2}} \right]_3^4=-\frac{16\pi}{3}\left(0-1 \right)=\frac{16\pi}{3}$$

Now, adding the two volumes, we find:

$$V=V_1+V_2=\frac{49\pi}{6}+\frac{16\pi}{3}=\frac{27\pi}{2}$$

This agrees with the result we found using the shell method.

To amanda and any other guests viewing this topic, I invite and encourage you to post other calculus questions here in our http://www.mathhelpboards.com/f10/ forum.

Best Regards,

Mark.