rudransh verma
Gold Member
- 1,067
- 96
- Homework Statement
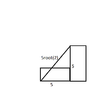
- A 2kg brick of dimension 5m*2.5m*1.5m is lying on the largest base. It is now made to stand with length vertical, then amount of work done is (g=10)
- Relevant Equations
- W=F.d
W=-mgd=2*10*1.5=30J. I don’t think this is right.
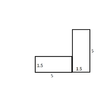
 . I took a corner and calculated how far that corner travels but for different corners its different.
. I took a corner and calculated how far that corner travels but for different corners its different.