- #1
BlackMelon
- 45
- 7
Hi All,
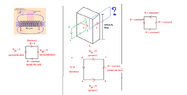
In the attachment, I have 3 scenarios in question.
The first one is just a solenoid from http://hyperphysics.phy-astr.gsu.edu/.
The second one is a hollow cuboid, which is infinitely long. I am using the same analogy as the solenoid. Would I be able to set the same Amperian loop?
For the third one, I do not have the circuits. If the magnetic field of each side of the loop is constant, but all the fields are not equal, would I be able to apply the Ampere's law?
Edited: In the scenario 2, why applying both green and blue loop at the same time (which results in the magnetic field twice of that of the green loop alone) is wrong?
Best Regards
In the attachment, I have 3 scenarios in question.
The first one is just a solenoid from http://hyperphysics.phy-astr.gsu.edu/.
The second one is a hollow cuboid, which is infinitely long. I am using the same analogy as the solenoid. Would I be able to set the same Amperian loop?
For the third one, I do not have the circuits. If the magnetic field of each side of the loop is constant, but all the fields are not equal, would I be able to apply the Ampere's law?
Edited: In the scenario 2, why applying both green and blue loop at the same time (which results in the magnetic field twice of that of the green loop alone) is wrong?
Best Regards
Attachments
Last edited: