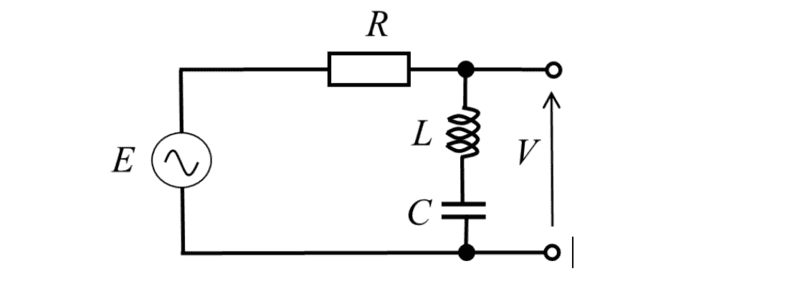
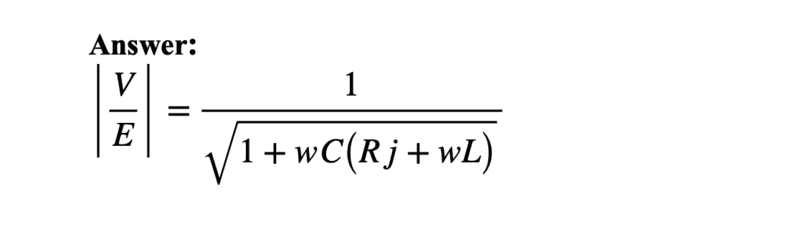The discussion revolves around the calculations related to the amplitude of an analog filter, specifically focusing on reactance and impedance. Participants emphasize the importance of correctly identifying the signs of capacitive and inductive reactance in calculations. There is a consensus that at resonance, the reactance should equal zero, leading to a deep notch in output voltage. The need for careful handling of complex numbers in impedance calculations is highlighted, particularly the use of the imaginary unit 'j' to maintain orthogonality between real and imaginary components. Overall, the conversation underscores the necessity of methodical approaches in electrical engineering calculations.