snypehype46
- 10
- 1
- Homework Statement
- Calculate the amplitude of this Feynman diagram in momentum space for $\phi^4$ theory
- Relevant Equations
- None
This is not really homework assigned to me but I wasn't sure where to post this.
I'm trying to work through the book "Quantum Field Theory for Gifted Amateurs" by Tom Lancaster. I'm doing the questions on Chapter 19 to understand how to draw Feynman diagrams and work out their amplitude. One of the exercises involved the computation of the amplitude of the following Feynman diagram in momentum space:
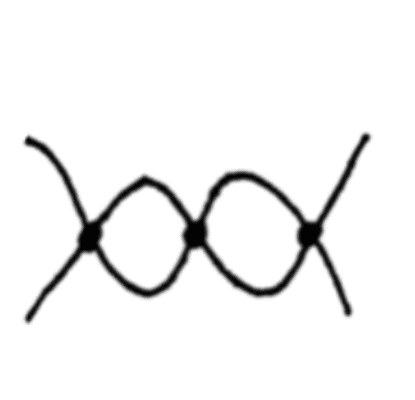
What I got was the following:
$$2\pi ^4 \delta^{(4)} (p_1+p_2- q_1 -q_2) \frac{(-i \lambda)^3}{4} \int {\frac{d^4 k_1 d^4 k_2 d^4 k_3 d^4k_4}{(2\pi)^16}}
\frac{i}{k_1^2 -m^2 +i\epsilon}
\frac{i}{k_2^2 -m^2 +i\epsilon} \times \\
\frac{i}{(p_1 +p_2 - k_3)^2 -m^2 +i\epsilon}
\frac{i}{(p_1 +p_2 - k_4)^2 -m^2 +i\epsilon}
$$
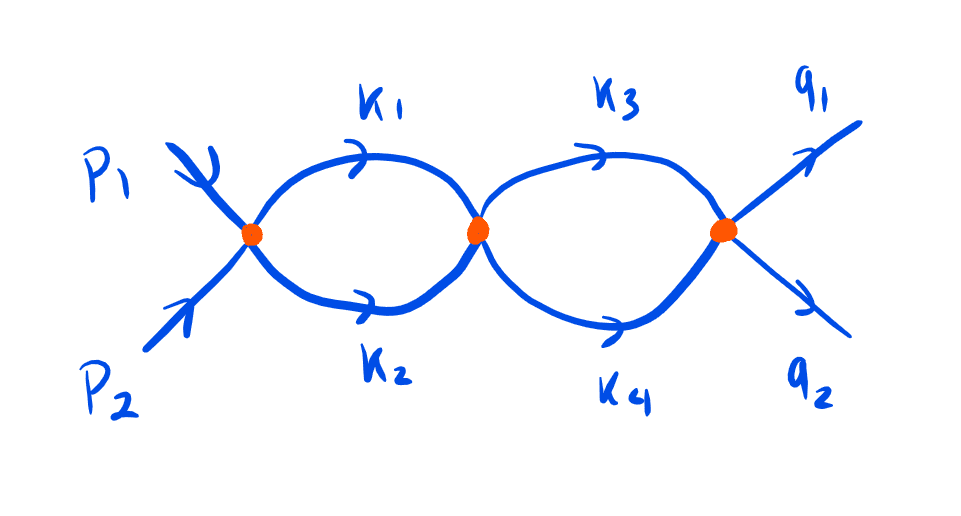
This is the diagram I drew to compute this
But it turns that the correct solution should be
$$2\pi ^4 \delta^{(4)} (p_1+p_2- q_1 -q_2) \frac{(-i \lambda)^3}{4} \int {\frac{d^4 k_1 d^4 k_2}{(2\pi)^8}}
\frac{i}{k_1^2 -m^2 +i\epsilon}
\frac{i}{k_2^2 -m^2 +i\epsilon} \times \\
\frac{i}{(p_1 +p_2 - k_1)^2 -m^2 +i\epsilon}
\frac{i}{(p_1 +p_2 - k_2)^2 -m^2 +i\epsilon}
$$
I don't quite get how to get rid of the ##k_3## and ##k_4## terms as they did in the solution. I assume this is due to the conservation of momentum but I'm not sure.
I'm trying to work through the book "Quantum Field Theory for Gifted Amateurs" by Tom Lancaster. I'm doing the questions on Chapter 19 to understand how to draw Feynman diagrams and work out their amplitude. One of the exercises involved the computation of the amplitude of the following Feynman diagram in momentum space:
What I got was the following:
$$2\pi ^4 \delta^{(4)} (p_1+p_2- q_1 -q_2) \frac{(-i \lambda)^3}{4} \int {\frac{d^4 k_1 d^4 k_2 d^4 k_3 d^4k_4}{(2\pi)^16}}
\frac{i}{k_1^2 -m^2 +i\epsilon}
\frac{i}{k_2^2 -m^2 +i\epsilon} \times \\
\frac{i}{(p_1 +p_2 - k_3)^2 -m^2 +i\epsilon}
\frac{i}{(p_1 +p_2 - k_4)^2 -m^2 +i\epsilon}
$$
This is the diagram I drew to compute this
But it turns that the correct solution should be
$$2\pi ^4 \delta^{(4)} (p_1+p_2- q_1 -q_2) \frac{(-i \lambda)^3}{4} \int {\frac{d^4 k_1 d^4 k_2}{(2\pi)^8}}
\frac{i}{k_1^2 -m^2 +i\epsilon}
\frac{i}{k_2^2 -m^2 +i\epsilon} \times \\
\frac{i}{(p_1 +p_2 - k_1)^2 -m^2 +i\epsilon}
\frac{i}{(p_1 +p_2 - k_2)^2 -m^2 +i\epsilon}
$$
I don't quite get how to get rid of the ##k_3## and ##k_4## terms as they did in the solution. I assume this is due to the conservation of momentum but I'm not sure.
Last edited: