An Aspect of Lemma 3.3 .... Laczkovich and Vera T Sos .... L&S ....

[Math Amateur]

I am reading Chapter 3: Jordan Measure ... of Miklos Laczkovich and Vera T Sos's book "Real Analysis: Series, Functions of Several Variables, and Applications" (Springer) ...

I need help with an aspect or step of the proof of Lemma 3.3 ... ...

The statement and proof of Lemma 3.3 of L&S reads as follows:

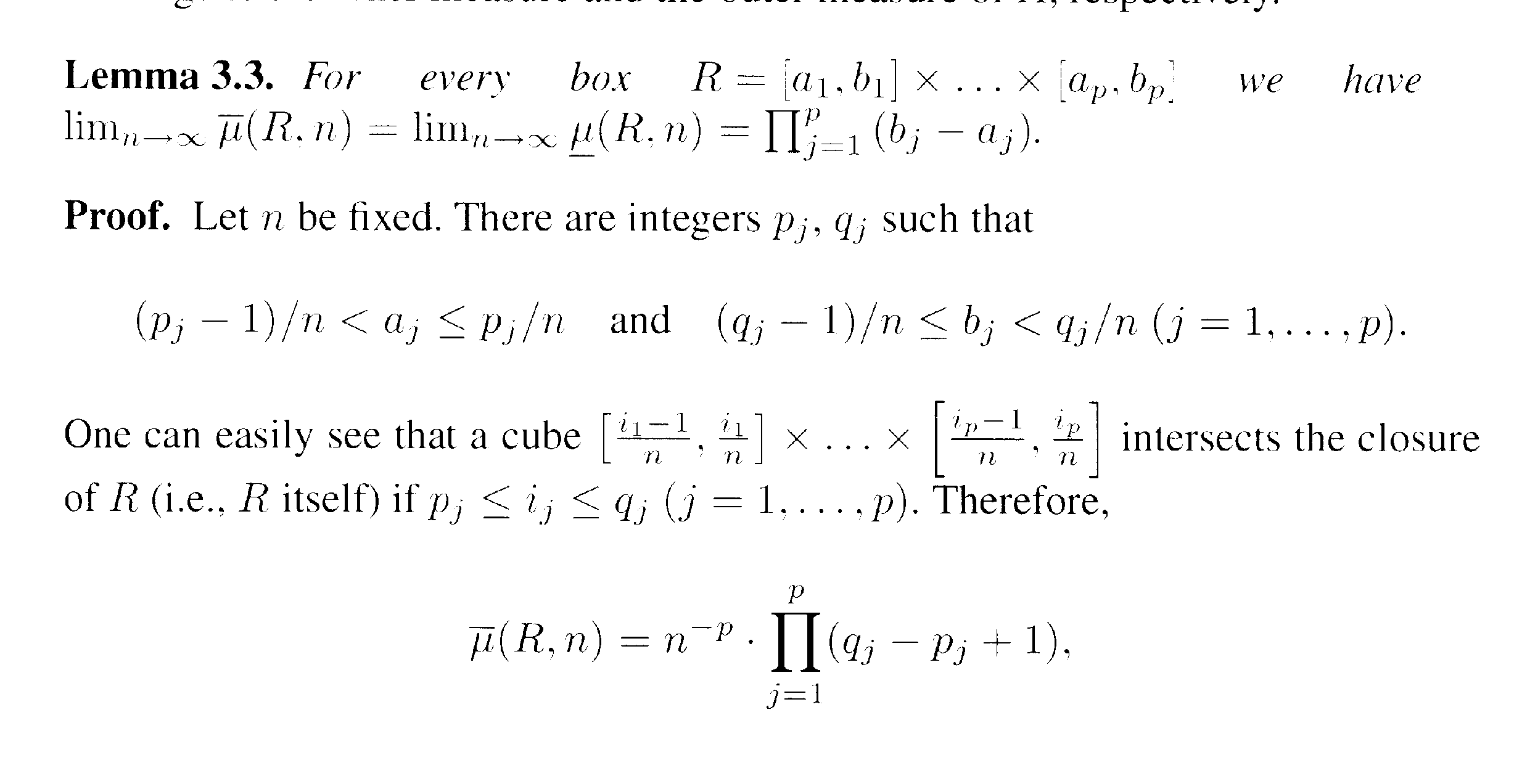
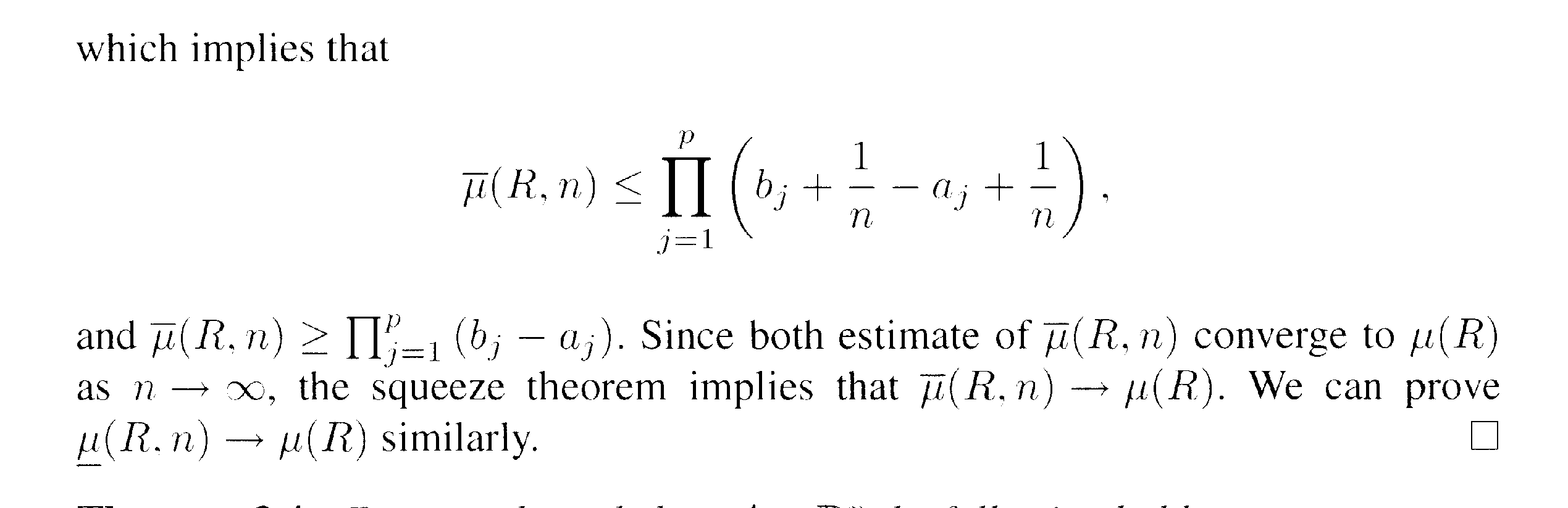
All the necessary definitions together with an explanation of the notation of Lemma 3.3 are given in the scan below ...



In the proof of Lemma 3.3 we read the following:

" ... ... Therefore


\(\displaystyle \overline{ \mu } (R,n) = n^{ -p} \prod_{ j =1}^p (q_j - p_j + 1 ) \) ... ... ... "


Can someone please help me to prove this ... as yet i have been unable to make a meaningful start on this ...



Help will be appreciated ...

Peter



NOTE:

To make sense of Lemma 3.3 readers of the above post will need access to pages 95-97 of L&S so I providing this text as follows:

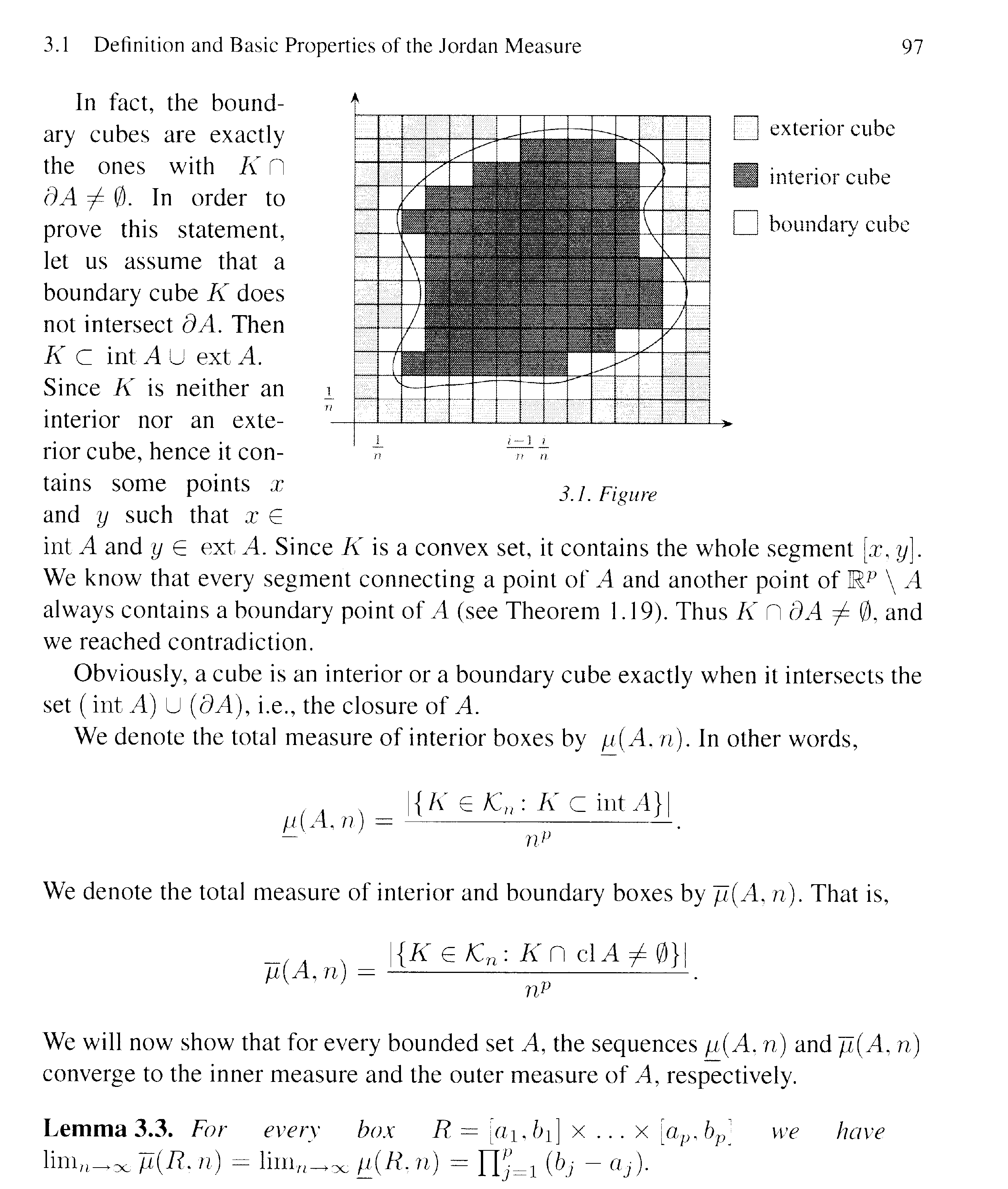
Hope that helps ...


Peter

 

[jvicens]

, I am happy to assist you with understanding and proving Lemma 3.3. Let's start by breaking down the statement and notation used in the proof.

First, we have the notation of $\overline{\mu}(R,n)$ which represents the upper Jordan measure of the set $R$ with respect to the partition $n$. This is defined as the sum of the volumes of the subrectangles in the partition $n$ that intersect with the set $R$, where each subrectangle has a volume of $n^{-p}$.

Next, we have the product notation, which represents the product of $p$ terms. In this case, the terms are $(q_j - p_j + 1)$, where $q_j$ represents the upper bound of the $j$th interval in the partition $n$ and $p_j$ represents the lower bound of the same interval.

Now, let's look at the statement of Lemma 3.3. It states that the upper Jordan measure of a set $R$ is equal to the product of the lengths of the intervals in the partition $n$ that intersect with $R$. This can be seen by breaking down the product notation as follows:

$$\prod_{j=1}^p(q_j-p_j+1) = (q_1-p_1+1)\cdot(q_2-p_2+1)\cdot...\cdot(q_p-p_p+1)$$

Each term in this product represents the length of an interval in the partition $n$, and when multiplied together, they give us the total volume of the subrectangles in the partition $n$ that intersect with $R$. Multiplying this by $n^{-p}$ gives us the total volume of the subrectangles, which is equal to the upper Jordan measure of $R$.

To prove this statement, we can use the definition of upper Jordan measure and the properties of products. We know that the upper Jordan measure of a set $R$ is equal to the sum of the volumes of the subrectangles in the partition $n$ that intersect with $R$. Using the definition of volume, we can write this as:

$$\overline{\mu}(R,n) = \sum_{j=1}^p(n^{-p})(q_j-p_j+1)$$

We can now use the properties of products to rewrite this as a product, as follows:

$$\overline{\