An object with mass m moving on x'x and Ep(x) = (1/2)*k*(x^2 - 4)^2

[Michael_0039]

Homework Statement

An object with m mass moving on x'x and Ep(x) = (1/2)*k*(x^2 - 4)^2 . x is the position of the object and k>0 (constant)

The object starts with zero velocity from x0=1

1) V(max) = ? and X @ V(max)
2) Which is the position speed will be zero again ?

Relevant Equations

nil

Hi !

This is my try:

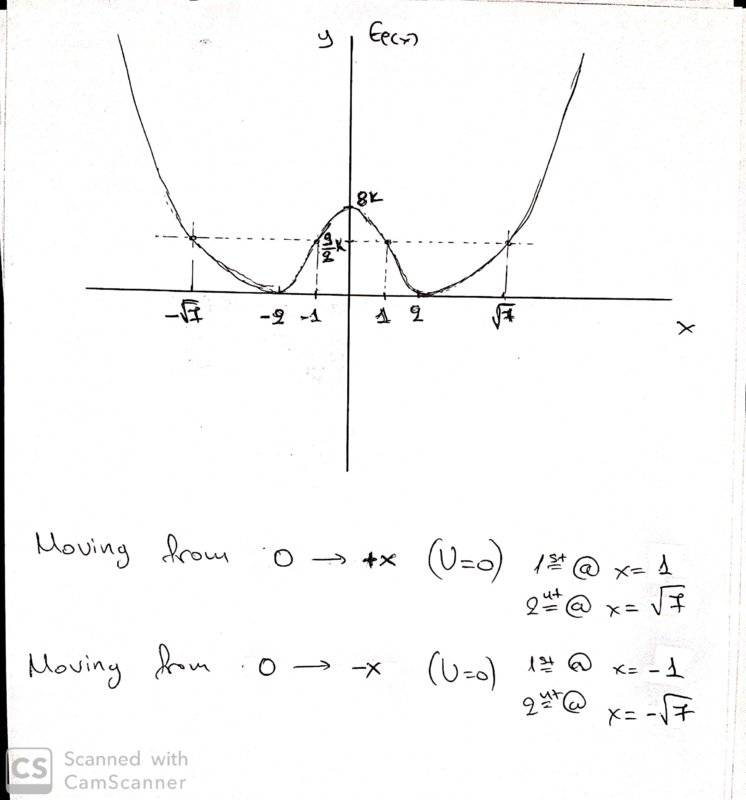Is that correct ?

Thanks

 

[tnich]

Almost correct. All of your calculations are right, but you need to figure out which solutions for $v=0$ can actually happen. How much total energy would be required for the system to achieve $x=0$? What would be the velocity at that point if the total energy is $\frac 9 2 k$?

 

[haruspex]

In addition to @tnich's observation, I have a minor comment. Your sketch is a little out of scale. Which two of the x positions 1, 2, √7 should be closest together?