- #1
DennisN
Gold Member
2023 Award
- 2,091
- 8,642
- TL;DR Summary
- Is this scenario regarding an observer passing a black hole event horizon reasonable or incorrect?
Hi all, this is a new scenario I got thinking about after having received great feedback and corrections from other PF'ers in this thread. Thanks again for the great help! This new scenario is similar to the previous one, but with a twist including a mirror. And as I said in that thread, I am not particularly well aquainted with GR.
First, the assumptions:
Scenario: Laser, Mirror and Observer.
An observer is sitting at the left side in a container which is heading left towards an event horizon.
The observer is holding a turned on laser pointer that is directed at a vertical mirror that is located at the right side of the container. The observer can thus observe the laser light since it is reflected by the mirror back towards the observer.
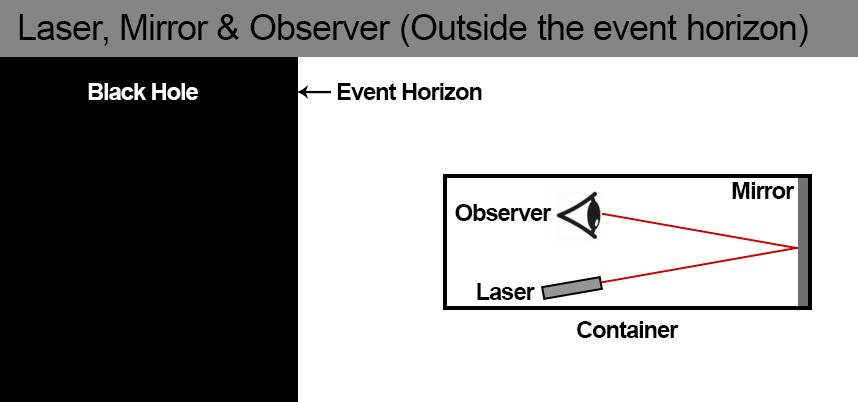
Picture 1. Laser, observer & mirror are outside the event horizon.
The observer observes the laser light reflected by the mirror.
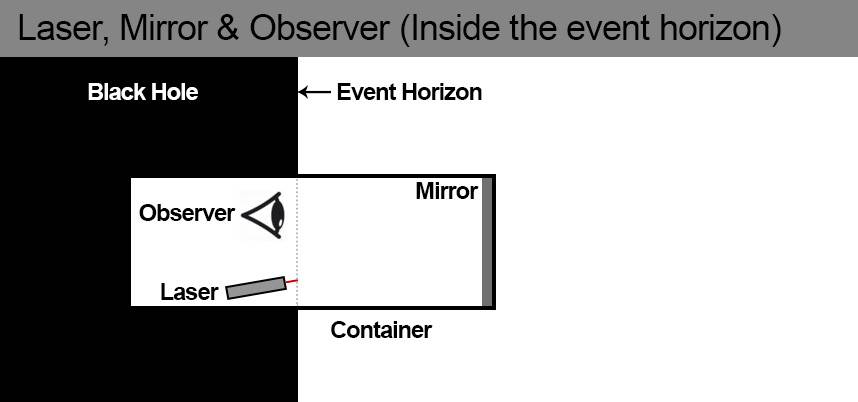
Picture 2. Laser & observer are inside the event horizon, mirror is still outside the event horizon.
As the observer and laser passes the event horizon, I am pretty sure that no more (new) light from the laser can reach the mirror and get reflected back to the observer. Thus it seems reasonable that the observer sees no more light. Now, of course light travels at c, so there may be a very brief moment the observer sees the remaining light after the laser passes the event horizon, but after this it seems to me the observer will not see any more light from the laser.
3. (no picture) Laser, observer & mirror are inside the event horizon.
As the right side of the container and thus the vertical mirror finally passes the event horizon, it seems to me that the observer will still not see any laser light, since the light going towards the right can't overcome the spacetime curvature.
Is this scenario reasonable, and if not, where am I thinking wrong?
Cheers!
-------------------------------------------------------------------------------------------------
(A personal note from me:
I'd like to add that I don't have an agenda to show that an observer notices passing an event horizon, I have been and still am perfectly fine with the opposite. The reason I'm posting the scenario is because (1) for some reason I've been thinking about event horizons lately and (2) I don't trust myself to think correctly about the scenario and (3) I'm always happy to get a better understanding of things I don't understand so well.
To add some spice to the scenario, the poor observer can be called "Muerte", sitting in a container called "Pasta" since it will eventually be turned into spaghetti. :) Figuratively, at least. And thus the dish that is served closer to the singularity is called "Pasta Muerte". Bon appetit!
(I actually have one more scenario I can't figure out with regards to the event horizon, but it's
completely different and hasn't anything to do with if an observer notices passing it. Therefore
I may post it in another thread later when I've understood this one.)
First, the assumptions:
- The black hole is massive enough that there are no significant tidal forces near nor at the event horizon.
- There is no firewall nor quantum effects at the event horizon, i.e. only standard GR is assumed.
- The container and its contents is in free fall and is doomed to pass the event horizon.
Scenario: Laser, Mirror and Observer.
An observer is sitting at the left side in a container which is heading left towards an event horizon.
The observer is holding a turned on laser pointer that is directed at a vertical mirror that is located at the right side of the container. The observer can thus observe the laser light since it is reflected by the mirror back towards the observer.
Picture 1. Laser, observer & mirror are outside the event horizon.
The observer observes the laser light reflected by the mirror.
Picture 2. Laser & observer are inside the event horizon, mirror is still outside the event horizon.
As the observer and laser passes the event horizon, I am pretty sure that no more (new) light from the laser can reach the mirror and get reflected back to the observer. Thus it seems reasonable that the observer sees no more light. Now, of course light travels at c, so there may be a very brief moment the observer sees the remaining light after the laser passes the event horizon, but after this it seems to me the observer will not see any more light from the laser.
3. (no picture) Laser, observer & mirror are inside the event horizon.
As the right side of the container and thus the vertical mirror finally passes the event horizon, it seems to me that the observer will still not see any laser light, since the light going towards the right can't overcome the spacetime curvature.
Is this scenario reasonable, and if not, where am I thinking wrong?
Cheers!
-------------------------------------------------------------------------------------------------
(A personal note from me:
I'd like to add that I don't have an agenda to show that an observer notices passing an event horizon, I have been and still am perfectly fine with the opposite. The reason I'm posting the scenario is because (1) for some reason I've been thinking about event horizons lately and (2) I don't trust myself to think correctly about the scenario and (3) I'm always happy to get a better understanding of things I don't understand so well.
To add some spice to the scenario, the poor observer can be called "Muerte", sitting in a container called "Pasta" since it will eventually be turned into spaghetti. :) Figuratively, at least. And thus the dish that is served closer to the singularity is called "Pasta Muerte". Bon appetit!
(I actually have one more scenario I can't figure out with regards to the event horizon, but it's
completely different and hasn't anything to do with if an observer notices passing it. Therefore
I may post it in another thread later when I've understood this one.)