An odd result from integrating to calculate the age of the Universe

[Buzz Bloom]

TL;DR Summary

I have been interested in finding a way to use an online integration tool to calculate the age of the universe. The answer I got is clearly wrong. I am hoping someone will be able to help me find my error.

The integration tool I am using is
https://www.symbolab.com/solver/definite-integral-calculator .

The following are the values of the five variables in the Friedmann equation with references of sources. I have also defined single letter variables I used for convenience.
http://www.thesuperspark.com/2015/07/age-of-universe-144-billion-years.html
J = 1/H_0 = 14.4 billion years.

https://astronomy.stackexchange.com/questions/19393/latest-cosmological-parameters
R = Omega_r = 0.0000905

https://www.cosmos.esa.int/documents/387566/387653/Planck_2018_results_L06.pdf page 33 eq 35
M = Omega_m = 0.3081

https://www.cosmos.esa.int/documents/387566/387653/Planck_2018_results_L06.pdf page 40 eq 47b
K = Omega_k = 0.00007
(Thanks to PeterDonis for pointing out my former page number error.)

L = Omega Lambda = 1 - Omega_r - Omega_m - Omega_k

The modified form below is based on the Friedmann equation integration:
https://en.wikipedia.org/wiki/Friedmann_equations#Detailed_derivation page .
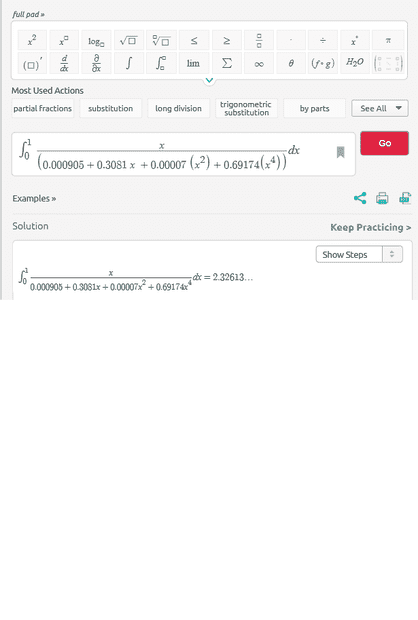
t/J = t H_0 = INTEGRAL[0,1] (x (R + M x + K x^2 + L x^4)^-0.5) dx

This integral should result in a value close to 1, since t is the age of the universe, and the value of J=1/H_0 is close to (but not exactly equal to) this age.

The value of the calculated integral is 2.32613.

 

[PeterDonis]

page 30 eq 47b
K = Omega_k = 0.00007

I think you meant page 40, since that's where equation 47b appears.

 

[PeterDonis]

The value of the calculated integral is 2.32613

I think the site was misinterpreting what you input because of the parentheses around $x^2$ and $x^4$; it seems to be very fussy about formatting.

When I tried it I got 0.95652:

 

[PeterDonis]

When I tried it I got 0.95652

I get the same answer using scipy's integration:

>>> from math import sqrt
>>> R = 0.0000905
>>> M = 0.3081
>>> K = 0.00007
>>> L = 1 - R - M - K
>>> L
0.6917395
>>> def f(x):
...     return x / sqrt(R + M * x + K * x**2 + L * x**4)
...
>>> import scipy.integrate
>>> scipy.integrate.quad(f, 0, 1)
(0.9565205740691728, 6.564259555787992e-10)

 

[PeterDonis]

When I tried it I got 0.95652

And that number times 14.4 billion gives 13.8 billion, which is our current estimate of the actual age of the universe. So this value makes sense.

 

[Buzz Bloom]

Hi PeterDonis:

Thank you very much for your help. Unfortunately I tried to copy what you did and ran the integration tool again with the revised form, but it failed.

Regards,
Buzz

 

[PeterDonis]

Unfortunately I tried to copy what you did

I don't think copying and pasting will work with that tool. As I said, it appears to be extremely fussy about formatting. I think you have to start from scratch and build the integrand using the site's own formatting tools, just don't put parentheses around the $x^2$ and $x^4$ terms under the square root. That's how I had to do it; any cutting and pasting I did didn't work.

One reason I prefer using Python for this is that it's a lot easier to type functions in Python notation, which boils down to plain text, than to have to use some website designer's idea of "helping" me to format an expression.

 

[PeterDonis]

it failed

I got the "steps are currently not supported for this problem" error a couple of times myself while I was trying to get the expression properly formatted. Another serious flaw with that website is that you can't tell just from looking at the expression it's displaying exactly how the code is going to parse the expression; it could be reading it differently from how it appears and there's no way to know it until you press "Go" and get an error like that one. I had to re-start the expression from scratch a couple of times because of that.

 

[Buzz Bloom]

Hi @PeterDonis:

I tried again and got he tool to give me an answer. Unfortunately it is not the right answer.

Regards,
Buzz

 

[Ibix]

The last term in your last image says $x^3$, but it should be $x^4$.

 

[Buzz Bloom]

The last term in your last image says x^3, but it should be x^4.

Hi @Ibix:

Thank you very much for the correction. I finally got the right result. I apologize for my incompetence which I entirely blame on my advanced aging years.

Regards,
Buzz

 

[Ibix]

I'm a good few years younger than you and I make stupid typos all the time.

I'm guessing you're new to computer programming (which I would say is what you're doing when setting up this integrator). Typos can be difficult to spot, and they're probably the number one source of bugs in code. The lesson to learn here is that all too often we make simple mistakes inputting data or instructions, and double- and triple-checking what you've typed is vital.

 

[PeterDonis]

computer programming (which I would say is what you're doing when setting up this integrator)

Actually the person who set up the website in question was doing the programming, and doing it badly IMO. The way the site forces you to enter your integral and the way it displays things makes it very difficult to get the entry right. Note that in the second attempt the OP posted, there were no typos at all, yet it didn't work correctly. IMO that's the fault of the website's programmer, not the OP. (And you would see even more instances if I had posted images of every try I made on that website before I got the integral to work correctly.)

 

[PeterDonis]

I think the site was misinterpreting what you input because of the parentheses around and ; it seems to be very fussy about formatting.

Actually, on looking at the first attempt again, there is no square root in the denominator.

 

[Ibix]

Actually the person who set up the website in question was doing the programming,

I guess it depends what you call programming. I'd call using a numerical integrator at least scripting, even if not outright programming. Whatever you call it, the point is that you are entering instructions that the computer is supposed to execute and it doesn't have the background knowledge it needs to correct typos which are easy to make even with a friendly interface. So (whether you get the result you expect or not!) check first for stupid daya entry errors, because they happen a lot.

and doing it badly IMO. The way the site forces you to enter your integral and the way it displays things makes it very difficult to get the entry right.

Good UIs are hard to do, especially for something as flexible as equation entry. Harder than good numerical integrators, IMO.

 

[PeterDonis]

I'd call using a numerical integrator at least scripting, even if not outright programming.

To me, "programming" means you're entering text in some programming language, like the Python session that I posted earlier. If you're not entering text, but trying to fill in boxes created by a web UI, you're not programming IMO; you're just using a web interface (and in this case a badly designed one IMO).

Have you tried to use the website in question? If not, I suggest doing so. IMO it is nothing like programming or even scripting.

 

[Ibix]

To me, "programming" means you're entering text in some programming language, like the Python session that I posted earlier.

Two of the tools I use at work let you write programs by dragging and dropping boxes and connecting them, with some use of a text editor to specialise the behaviour of some boxes. One of those is much better than the other and both are generating text instructions in the background, but I'd say that was programming. So I'm not really sure that there's much of a distinction between giving scipy.integrate a function and giving some web interface a function except the entry method. Obviously you can build a lot more around the python version (and that's where real programming starts, which is why I was suggesting calling this scripting), but it's possible that what the website does in the background is translate its input to python code and feed it into scipy.integrate, which would look pretty much like what you wrote.

I certainly agree that this interface is rubbish. I made a typo and entered 0.000905 (one 0 too few) and got an answer (obviously not the correct one), but adding the extra zero causes it to die with "steps are currently not supported for this problem". Not sure what's going on there...

 

[PeterDonis]

Two of the tools I use at work let you write programs by dragging and dropping boxes and connecting them, with some use of a text editor to specialise the behaviour of some boxes. One of those is much better than the other and both are generating text instructions in the background, but I'd say that was programming.

I would say the actual programming was done by whoever wrote the tools. But there is no single hard and fast definition of the term.

 

[Ibix]

I would say the actual programming was done by whoever wrote the tools. But there is no single hard and fast definition of the term.

Fair enough, but then I'd say your python program isn't really programming either. You just gave it a string of text which the python compiler processed and fed into the integrator that someone else wrote. It seems to me like the line between "just using tools someone else wrote" and "actually programming" is more about the complexity of what you do with those tools than the input method.

But as you say, there isn't a hard and fast rule, so it's a bit like the argument over "what is a frame in relativity". And we're pretty far off topic anyway, so I'll leave it here.

 

[PeterDonis]

then I'd say your python program isn't really programming either.

You could call that "scripting" instead of "programming", yes. And of course every programming language is itself a tool that someone else programmed. So there are always multiple levels involved and there aren't clean breaks between one thing and another.

 

[Buzz Bloom]

Hi @ibis:

I had a career as a applied mathematician and software developer for over 40 years before I retired. My aging problem is that I do not spot my errors very well no matter how hard I try. In my working years I was quite good at that.

Regards,
Buzz

 

[Ibix]

I see.

Try entering it twice and comparing? It's a bit brute force, but if it works... I actually spotted your mistake by pasting your and Peter's screenshots into a paint program one above the other and going character-by-character.