Analyse motion of an oscillator: x(t)=0.2cos(12*pi*t)

[MatinSAR]

Homework Statement

The equation of motion of an oscillator in SI is $x(t)=0.2cos(12\pi t)$. In the time interval $(\frac {1}{18}s,\frac {2}{3}s)$, How many seconds is the speed increasing?

Relevant Equations

Kinematics.

Hello.
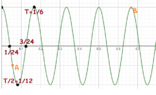
I have tried to solve it using x-t Graph. We know that period of this function is $T=\frac {1}{6}s$.
Then I've used $x(t)=0$ to find the times in which the oscillator is at $x=0$:
$t=\frac {k}{12} + \frac {1}{24}$ for $k \in Z.$
Now I can draw x-t graph.

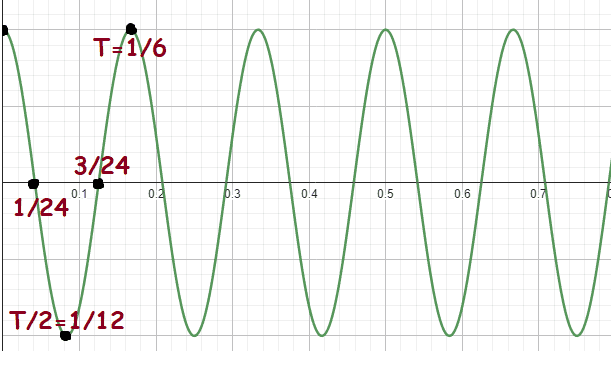
We should check time interval $(\frac {1}{18}s,\frac {2}{3}s)$:
$x(\frac {1}{18}s)=-0.1m$ (Point A in below graph.)
$x(\frac {2}{3}s)=0.2m$ (Point B in below graph.)

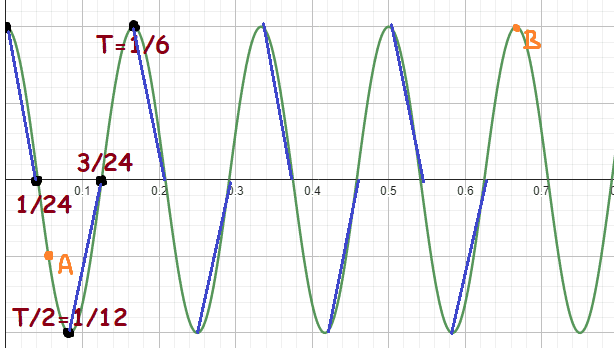
Blue lines show motion with increasing speed.
So time of motion with increasing speed is: $(7)(\frac {3}{24}s-\frac {2}{24}s)= \frac {7}{24}s.$

Is it correct?
Can someone suggest another easy way please?

 

[SammyS]

Consider the time interval from $t=1/12$s to time $t=2/3$s. During one half of this interval, the object's speed is increasing and during one half of the interval, it's decreasing.

 

[MatinSAR]

@sammy Thank you for your help.

Another way that came to my mind:
In a complete period, the speed is increasing in $T/2$ seconds.
First period is incomplete(I mean we should check time interval $(1/12,2/3s)$) but we can find that in this period the speed is increasing in $T/4$ seconds.
Here we have 3 complete periods plus one incomplete period. We put $T=1/6s$ then we have:
$(3)(T/2)+T/4=7T/4=7/24s$

 

[TSny]

Is it correct?
Can someone suggest another easy way please?

Your result looks correct to me and your method looks good.

Another approach is to note that the speed is increasing whenever the velocity and acceleration have the same sign. This is equivalent to saying that the product of the velocity and acceleration is positive.

You can easily show that the product of velocity and acceleration is equal to a positive constant times $\sin(24 \pi t)$. So, the speed is increasing whenever $\sin(24 \pi t)$ is positive. But, you still have to think about the beginning and ending times: 1/18 s and 2/3 s.

I don't think this approach is really any better. It's just a different way to think about it.

 

[haruspex]

Another approach is to note that the speed is increasing whenever the velocity and acceleration have the same sign. This is equivalent to saying that the product of the velocity and acceleration is positive.

You can easily show that the product of velocity and acceleration is equal to a positive constant times $\sin(24 \pi t)$. So, the speed is increasing whenever $\sin(24 \pi t)$ is positive. But, you still have to think about the beginning and ending times: 1/18 s and 2/3 s.

Taking that a bit further, the product is positive for half the time in any interval of 1/12s, so it is a matter of figuring out the time for which it is positive in (0, 1/18), then subtracting that from half of 8/12.

 

[MatinSAR]

Your result looks correct to me and your method looks good.

@TSny Thank you for your time.

I don't think this approach is really any better. It's just a different way to think about it.

Thank you for sharing this.

@haruspex Thank you for your help.