Guillem_dlc
- 188
- 17
- Homework Statement
- The bent bar ##ABDE## is supported by spherical plain bearings at ##A## and ##E## and by the cable ##BF##. If a load of ##600\, \textrm{N}## is applied at ##C##, as shown in the figure, determine the tension in the cable.
Solution: ##853\, \textrm{N}##
- Relevant Equations
- Static equations, trigonometry
Figure:
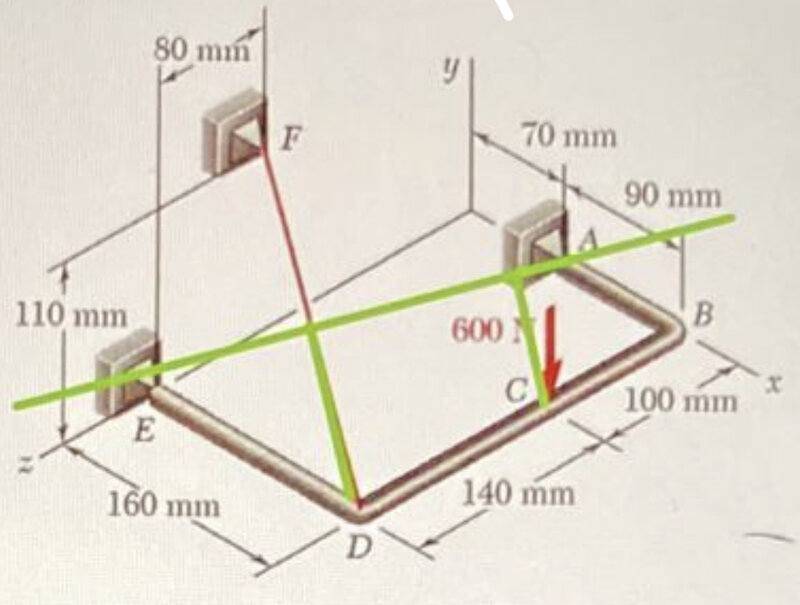
My attempt at a Solution:
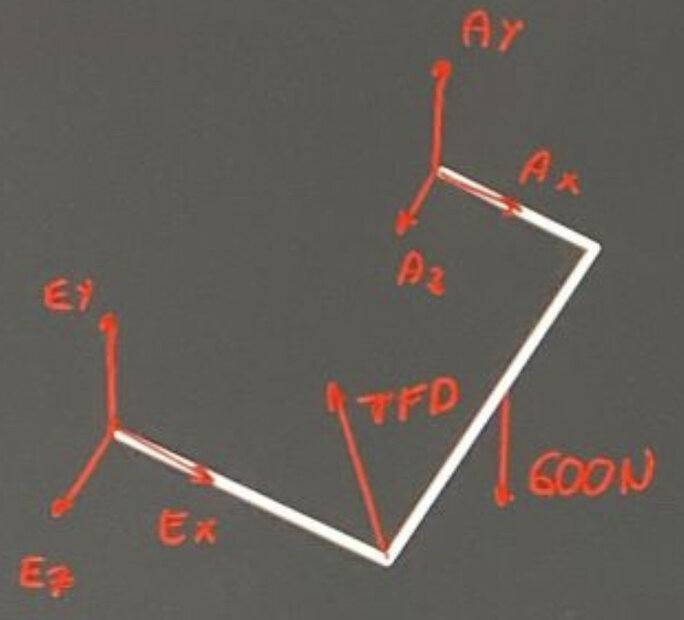
$$\overrightarrow{TFD}=TFD\dfrac{(-0,16\widehat{i}+0,11\widehat{j}-0,08\widehat{k})}{0,21}$$
View from above:
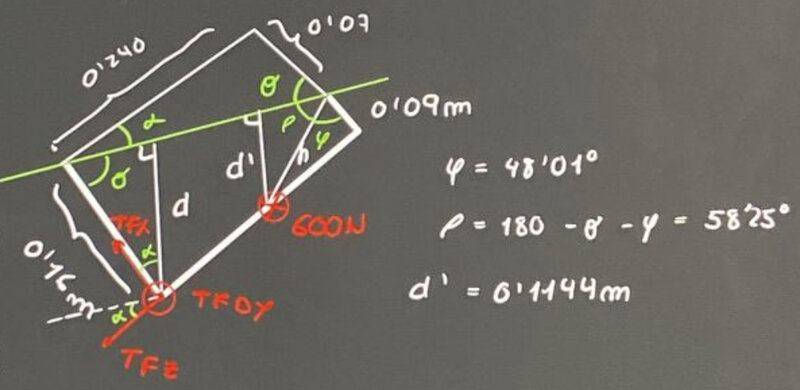
We calculate ##D##:
$$\sigma =90-\arctan \left( \dfrac{0,07}{0,240}\right)=73,74\, \textrm{º}$$
$$d=0,16\cdot \sin (\sigma)=0,1536\, \textrm{m}$$
##TF_x## does not make moment and ##TF_z## does not make time ##\rightarrow \alpha =16,26\, \textrm{º}##
$$\sum M_{EA}=TF_x\cdot \sin \alpha \cdot d+TF_z\cdot \cos \alpha \cdot d+TF_yd -600\cdot d'$$
$$\rightarrow TFD\dfrac{0,16}{0,21}\sin \alpha d+TFD\dfrac{0,08}{0,21}\cos \alpha d+TFD\dfrac{0,11}{0,21}d=600d'\rightarrow$$
$$\rightarrow TFD=\dfrac{0,21\cdot 600d'}{d}\cdot \left( \dfrac{1}{0,16\sin \alpha +0,08\cos \alpha +0,11}\right)=405,2\, \textrm{N}$$
Could you have a look at this one?
My attempt at a Solution:
$$\overrightarrow{TFD}=TFD\dfrac{(-0,16\widehat{i}+0,11\widehat{j}-0,08\widehat{k})}{0,21}$$
View from above:
We calculate ##D##:
$$\sigma =90-\arctan \left( \dfrac{0,07}{0,240}\right)=73,74\, \textrm{º}$$
$$d=0,16\cdot \sin (\sigma)=0,1536\, \textrm{m}$$
##TF_x## does not make moment and ##TF_z## does not make time ##\rightarrow \alpha =16,26\, \textrm{º}##
$$\sum M_{EA}=TF_x\cdot \sin \alpha \cdot d+TF_z\cdot \cos \alpha \cdot d+TF_yd -600\cdot d'$$
$$\rightarrow TFD\dfrac{0,16}{0,21}\sin \alpha d+TFD\dfrac{0,08}{0,21}\cos \alpha d+TFD\dfrac{0,11}{0,21}d=600d'\rightarrow$$
$$\rightarrow TFD=\dfrac{0,21\cdot 600d'}{d}\cdot \left( \dfrac{1}{0,16\sin \alpha +0,08\cos \alpha +0,11}\right)=405,2\, \textrm{N}$$
Could you have a look at this one?