FEAnalyst
- 348
- 149
- TL;DR Summary
- Is my approach to analytical verification of this finite element analysis correct ? What causes the difference ?
Hi,
I'm working on a simple FEA involving a preloaded bolt:
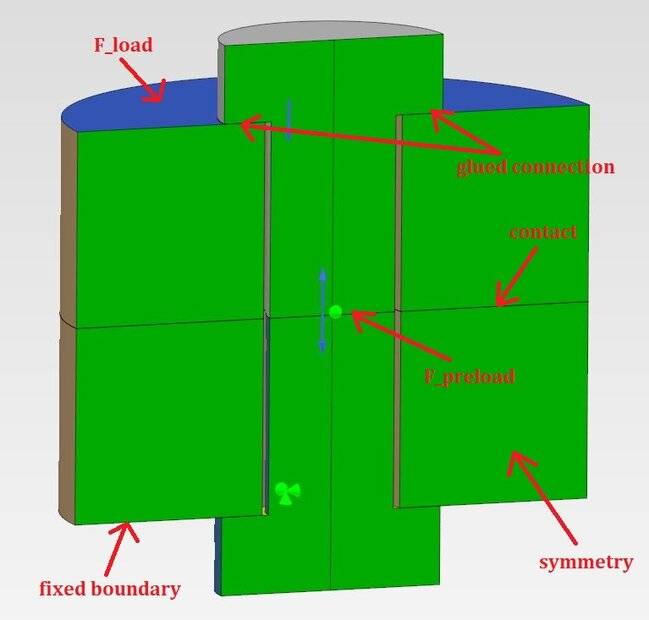
The bolt is modeled as a single part (shank + head + nut), glued (perfect bonding) to both rings. Pretension force ##F_{preload}=200 \ N## is applied in the first step of the analysis while in the second, pretension force stops working and actual compressive load ##F_{load}=400 \ N## is applied to the top surface of the top ring. The bottom surface of the bottom ring is fixed in all degrees of freedom. As you can see, the model utilizes symmetry. I get some results but my goal is to verify them using simple analytical calculations. Assuming that the bolt is just a bar under tension and then compression, I get from superposition: $$\sigma=\frac{F_{preload}}{A_{bolt}}-\frac{F_{load}}{A_{ring}}$$ where: ##A_{bolt}=155.3 \ mm^{2}## - area of half of the bolt's cross-section (to which preload force is applied), ##A_{ring}=2160 \ mm^{2}## - area of the top surface of the top ring (to which actual load is applied). Thus, I get: $$\sigma=1.1026 \ MPa$$ $$F=\sigma \cdot A_{bolt}=171.24 \ N$$ while from FEA I obtain around ##188 \ N##. What can be wrong here ? Are my assumptions for the analytical calculations incorrect ? I know that I should probably use higher values but for now, it's just about figuring out the correct approach.
I'm working on a simple FEA involving a preloaded bolt:
The bolt is modeled as a single part (shank + head + nut), glued (perfect bonding) to both rings. Pretension force ##F_{preload}=200 \ N## is applied in the first step of the analysis while in the second, pretension force stops working and actual compressive load ##F_{load}=400 \ N## is applied to the top surface of the top ring. The bottom surface of the bottom ring is fixed in all degrees of freedom. As you can see, the model utilizes symmetry. I get some results but my goal is to verify them using simple analytical calculations. Assuming that the bolt is just a bar under tension and then compression, I get from superposition: $$\sigma=\frac{F_{preload}}{A_{bolt}}-\frac{F_{load}}{A_{ring}}$$ where: ##A_{bolt}=155.3 \ mm^{2}## - area of half of the bolt's cross-section (to which preload force is applied), ##A_{ring}=2160 \ mm^{2}## - area of the top surface of the top ring (to which actual load is applied). Thus, I get: $$\sigma=1.1026 \ MPa$$ $$F=\sigma \cdot A_{bolt}=171.24 \ N$$ while from FEA I obtain around ##188 \ N##. What can be wrong here ? Are my assumptions for the analytical calculations incorrect ? I know that I should probably use higher values but for now, it's just about figuring out the correct approach.