- #1
amose093
- 4
- 0
I have recently completed my mid-year chemistry exam and came across a question that i cannot find an answer to. Me and my friends completely disagree and i was wondering if anyone could help me?
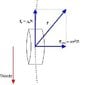
-The question showed a simplified diagram of a train around a circular section of a track, and the question asked-"draw an arrow representing the force exerted on the wheels of the train by the track while the train is decelerating".
Does the braking of the train have any effect on the forces present between the track and the train?
Thanx guys...
Andrew
-The question showed a simplified diagram of a train around a circular section of a track, and the question asked-"draw an arrow representing the force exerted on the wheels of the train by the track while the train is decelerating".
Does the braking of the train have any effect on the forces present between the track and the train?
Thanx guys...
Andrew