- #1
nafisanazlee
- 18
- 2
- Homework Statement
- Let a = 2i + j - 2k, b = i + j and c be a vector such that |c-a| = 3, | (a x b) x c| = 3 and the angle between c and a x b is 30°. Then, a.c is equal to?
- Relevant Equations
- a.b = |a||b|cosθ
|a×b| = |a||b|sinθ
The solution to the question is attached herewith. I approached in the exact same way and got |c| = 2. Then I thought like this:
the angle between a and a×b is 90°, and the angle between c and a×b is 30° (given). So one of the possibilities is, the angle between a and c is 90-30=60° degree. |a| = 3, and a.c gives me 2.3.cos60° = 3, which is not the correct answer. My question is, am I wrong in some way? Or the question has some problem in it?
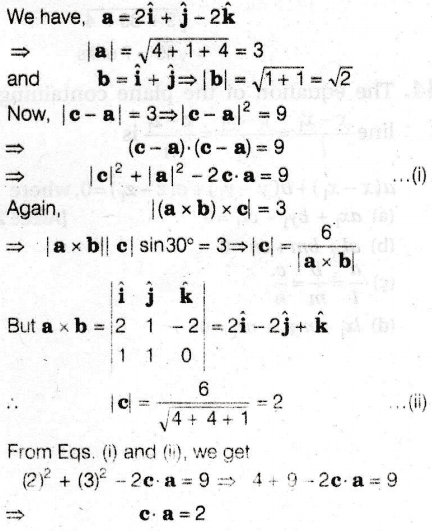
the angle between a and a×b is 90°, and the angle between c and a×b is 30° (given). So one of the possibilities is, the angle between a and c is 90-30=60° degree. |a| = 3, and a.c gives me 2.3.cos60° = 3, which is not the correct answer. My question is, am I wrong in some way? Or the question has some problem in it?
Last edited: