Angle of acceleration in non-uniform circular motion

[member 731016]

Homework Statement

Pls see below

Relevant Equations

Pls see below

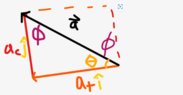
For (c),

Solution is

Can someone please explain how they calculated that angle? I thought they would do $arc\tan (\frac {32}{3.35})$

Many thanks!

 

[haruspex]

View attachment 322504
Can someone please explain how they calculated that angle? I thought they would do $arc\tan (\frac {32}{3.35})$

Many thanks!

$\tan^{-1}$ is one way of writing $\arctan$.
Or is it the 3.35/32 instead of the other way up that bothers you?

 

[Mark44]

$\tan^{-1}$ is one way of writing $\arctan$.
Or is it the 3.35/32 instead of the other way up that bothers you?

The OP seems to be unaware that the trig function inverses can be written in two ways: e.g., $\tan^{-1}(x)$ is the same as arctan(x), and similar for the other circular trig functions.

On another note, does anyone recognize the symbol that follows 5.98 in the solution? Evidently it means "degrees" since $\tan^{-1}(\frac{3.35}{32.0}) \approx 5.98$ (degrees), but the symbol used looks like $\gamma$ to me, which I've never seen used to signify degrees .

 

[member 731016]

$\tan^{-1}$ is one way of writing $\arctan$.
Or is it the 3.35/32 instead of the other way up that bothers you?

Thank you for your reply @haruspex!

Sorry I should been more accurate - it is the 3.35/32 that is bothering me

Many thanks!

 

[member 731016]

The OP seems to be unaware that the trig function inverses can be written in two ways: e.g., $\tan^{-1}(x)$ is the same as arctan(x), and similar for the other circular trig functions.

On another note, does anyone recognize the symbol that follows 5.98 in the solution? Evidently it means "degrees" since $\tan^{-1}(\frac{3.35}{32.0}) \approx 5.98$ (degrees), but the symbol used looks like $\gamma$ to me, which I've never seen used to signify degrees .

Thank you for your reply @Mark44!

Sorry I was actually aware that $tan^{-1} = arctan$. However, I was not sure why they wrote 3.35\32 instead 32\3.35 inside the tan function.

Also yeah that textbook solutions dose use the gamma symbol for degrees for some reason.

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

Sorry I should been more accurate - it is the 3.35/32 that is bothering me

Many thanks!

The 32 acceleration is radial. The angle quoted is that between the radial acceleration and the total acceleration. The cosine of that angle would be radial/total and its tangent is tangential/radial.

 

[member 731016]

The 32 acceleration is radial. The angle quoted is that between the radial acceleration and the total acceleration. The cosine of that angle would be radial/total and its tangent is tangential/radial.

Thank you for reply @haruspex !

When I draw a diagram of the accelerations acting on the mass when $\theta = 20~degrees$

Then draw a vector addition diagram to get the total acceleration,

I see that $\tan\theta = \frac{a_c}{a_t} = \frac{32}{3.35}$

I know this is bad practice to change symbols when solving a problem, but if I add an angle phi (use to represent tangent/radial acceleration) ,

Then I can see that $\tan\phi = \frac{a_t}{a_c}$. I think I'm now not sure how they got acceleration to be below the cord at 5.89 degrees.

Many thanks!

 

[haruspex]

View attachment 322528
Many thanks!

The angle of a line "below the cord" means the angle between the cord and the line, measured on the underside of the cord. In your last diagram above, that is the angle between the pale brown cord and the black total acceleration vector, measured anticlockwise from the cord.

 

[member 731016]

The angle of a line "below the cord" means the angle between the cord and the line, measured on the underside of the cord. In your last diagram above, that is the angle between the pale brown cord and the black total acceleration vector, measured anticlockwise from the cord.

Oh thank you for your help @haruspex! I see it now :)