- #1
Ben_Walker1978
- 113
- 6
- Homework Statement
- Find the Angle of twist and Shear stress in a shaft
- Relevant Equations
- Angle of twist and Shear stress in a shaft
Hello,
I have attempted the question below.
I think i have correctly completed the question.
Could anyone see if i have gone wrong?
As trying to learn this.
I am just worried about the units m to mm. Also the answer being correct, 917.6Gpa. I was unsure what units to use on the answer.
Question:
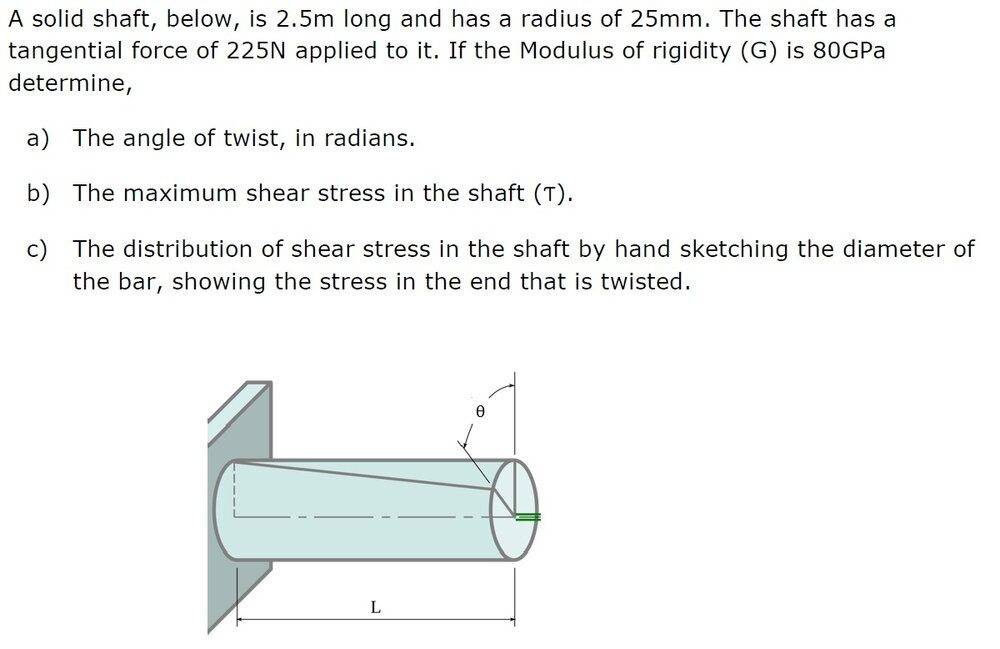 Answer:
Answer:

Any help much appreciated.
I have attempted the question below.
I think i have correctly completed the question.
Could anyone see if i have gone wrong?
As trying to learn this.
I am just worried about the units m to mm. Also the answer being correct, 917.6Gpa. I was unsure what units to use on the answer.
Question:
Any help much appreciated.