Angle of twist from in-plane displacements in FEA

[FEAnalyst]

TL;DR Summary

How to calculate the angle of twist from in-plane displacements?

Hi,

solid elements used in FEA don't have rotational DOFs so normally it's not possible to read the angle of twist from simulation involving torsion. Some programs allow the transformation of results to cylindrical coordinate system but it's not always the case. From what I've heard, it's possible to use in-plane displacement values to determine the angle of twist. However, I'm not sure how to actually do it. Here's an example of an elliptical bar subjected to torsion:
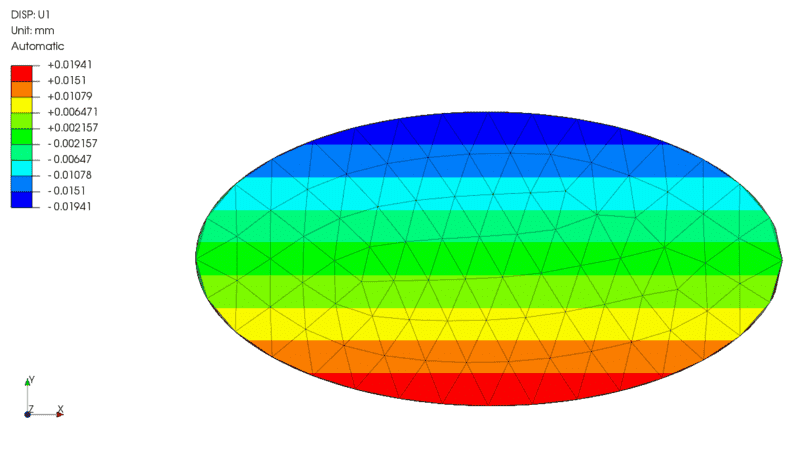
- X displacements:

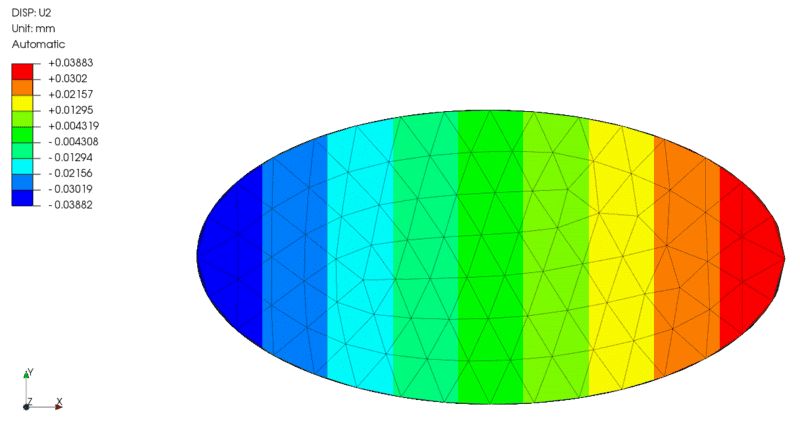
- Y displacements:

How can I calculate the angle of twist from these displacement values? Or maybe it's not enough and nodal coordinates are needed as well?

Thanks in advance for your help.

 

[jrmichler]

The maximum and minimum numbers in the color bars are the maximum X or Y displacement at the node with the maximum displacement. This is shown in the sketch below:

Note that the maximum Y displacement is exactly twice the maximum X displacement, and that the X dimension is twice the Y dimension of the ellipse. Also, the magnitudes of the positive X & Y displacements are equal to the magnitudes of the negative X & Y displacements. This shows that the total displacement is a rotation about the center of the ellipse. Any one of the displacements divided by its distance from the center gives the rotation angle in radians.

All of this is helped by the discretization which puts nodes at the extreme X and Y coordinates. Larger elements with nodes away from those points would add some error due to the lack of nodes at the extreme X and Y points on the ellipse.

It's easier to see this if the displacement plots are shown with deformed geometry.

 

[FEAnalyst]

Any one of the displacements divided by its distance from the center gives the rotation angle in radians.

Thank you very much. Let's take the displacement of the node on the left. The magnitude is $0.03882 \ mm$ and the semi-major axis is $100 \ mm$ so the angle should be $0.0003882 \ rad$. And the analytical value is $0.000394 \ rad$ so the results agree really well.

However, what about other types of cross-sections? Could I use the same method (nodal displacement divided by its distance from the center) for any other cross-section like rectangular for example ?

 

[jrmichler]

You should be able to if it has appropriate symmetry. Rectangular, hexagon, or hollow round tube should be good, while a C-channel would require more effort.

 

[FEAnalyst]

You should be able to if it has appropriate symmetry. Rectangular, hexagon, or hollow round tube should be good, while a C-channel would require more effort.

Right, asymmetric sections like C or L (probably also T) will be problematic here. Do you know how to calculate the angle of twist from in-plane displacements in such cases? Maybe different method should be used.
For example:
- cross-section:

- X displacement:

- Y displacement:

And the analytical result is $0.0257936508 \ rad$ in this case.

 

[jrmichler]

X displacement divided by distance from zero X displacement should be fairly close if the cross section maintains its shape. Similar for Y. Look at the deformed geometry plot, try some calculations, and find out.