- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
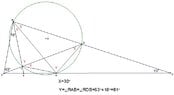
In a triangle $PQR$, $\angle P=84^{\circ}$, $\angle R=78^{\circ}$. Points $A$ and $B$ are on $PQ$ and $QR$ so that $\angle PRA=48^{\circ}$ and $\angle RPE=63^{\circ}$.
What is the measure of $\angle RAB$?
What is the measure of $\angle RAB$?