- #1
Garen
- 28
- 0
Homework Statement
The Attempt at a Solution
I thought I could take the second derivative and get the angular acceleration from which I could use
Garen said:Homework Statement

The Attempt at a Solution
I thought I could take the second derivative and get the angular acceleration from which I could usewhere ω is the angular velocity,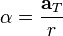 is the linear tangential acceleration, and r is the radius of curvature. But for some reason, it didn't give me the right answer, anyone know where I went wrong?
is the linear tangential acceleration, and r is the radius of curvature. But for some reason, it didn't give me the right answer, anyone know where I went wrong?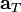
alphysicist said:Hi Garen,
Are you saying that you put in the tangential acceleration as your answer? If so, remember that they are asking for the total linear acceleration, and there is more to the total acceleration than just the tangential part.
Garen said:Oh, I thought that total linear acceleration was only the tangential acceleration...Would I have to include centripetal acceleration? If so, how?
alphysicist said:What is the formula for centripetal acceleration? (And remember that you have already found the angular velocity!)
Once you have found both components (the tangential and centripetal), the total is just the vector sum.
Garen said:I got it! Thanks a lot for your help.
Angular acceleration is the rate of change of angular velocity. It measures how quickly an object's angular velocity is changing over time.
Angular acceleration is calculated by dividing the change in angular velocity by the change in time. The formula for angular acceleration is α = Δω / Δt, where α is angular acceleration, Δω is the change in angular velocity, and Δt is the change in time.
Angular acceleration refers to the change in an object's rotational speed, while linear acceleration refers to the change in an object's linear speed. Angular acceleration is measured in radians per second squared, while linear acceleration is measured in meters per second squared.
Angular acceleration is directly proportional to the torque applied to an object. This means that the greater the torque, the greater the angular acceleration. The relationship between torque and angular acceleration is described by the equation α = τ / I, where α is angular acceleration, τ is torque, and I is moment of inertia.
Angular acceleration can be used to study the motion of objects that rotate, such as planets, gears, and wheels. It is also important in understanding the movement of objects in sports, such as the spin on a baseball or the rotation of a figure skater. Additionally, it is a crucial concept in the design and operation of machines and vehicles that involve rotational motion, such as cars and airplanes.