Angular frequency of two hanging bobs of different masses

[questionas]

Homework Statement

Two bobs (masses 2m and m) are suspended vertically by two equal springs k in series, shown below. Vertically coupled oscillators. To avoid confusion, let's call the TOP mass #1 and the BOTTOM mass #2 , as indicated. You may assume zero damping. Let's also agree to call the frequency ω0^2 = k/m.

(a) Show that the normal mode frequencies are ωf ≈ 1.307ω0 and ωs ≈ 0.541ω0, where f and s refer to fast and slow.

Relevant Equations

F=ma
F=-kx

This is a the representation of the two masses.

.
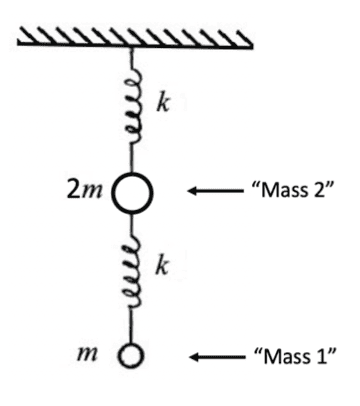Using Newton's second law I got the following equations assuming x1>>x2:
m*x1''(t) = -k(x1-x2)
m*x2''(t) = 0.5kx1-kx2

I put it in matrix form
m| x1''| = | -k k| *|x1|
|x2''| =| 0.5k -k| |x2|

After some simplification assuming the solution I Ae^iwt I got:
0 = | -k+mw^2 k | * |A1|
|0.5K -k+mw^2| |A2|

The I solve that the determinant M = 0
| -k+mw^2 k |
|0.5K -k+mw^2|

I got
w1 = sqrt( K/2m)
w2 = sqrt(3k/2m)

which is not the one the questions had.

 

[BvU]

Can you explain your first set of equations?

$\$

 

[Delta2]

Maybe the problem is that you totally neglect the weight force, each equation must be accompanied by a different weight ($-mg$ for the equation that contains $x_1''$, $-2mg$ for the other), I know in the case of simple vertical oscillation the weight doesn't affect the frequency of oscillation, not sure it works the same way here in coupled oscillation.

 

[Orodruin]

Maybe the problem is that you totally neglect the weight force, each equation must be accompanied by a different weight ($-mg$ for the equation that contains $x_1''$, $-2mg$ for the other), I know in the case of simple vertical oscillation the weight doesn't affect the frequency of oscillation, not sure it works the same way here in coupled oscillation.

This is just a constant addition to each force equation that can be removed by the addition of a constant (to the displacements). It does not effect the eigenfrequencies of the system. Which is why the approach

Can you explain your first set of equations?

is appropriate for helping the OP.

 

[Delta2]

Shouldn't the matrix have 0.5k ... -0.5k in the second row? Is that a typo or that's how you proceed in your original work?

 

[questionas]

Can you explain your first set of equations?

$\$

if your referring to the one where I applied Newton's second law, I assumed the system ws horizontal and that the mass 1 was pulled a distance x1 to the right and mass 2 was pulled a distance x2 to the right. Then the spring between the two masses would be stretched and that spring will pull mass 1 to the left hence the -k(x1-x2). Whereas mass 2 will be pulled to the right by the same spring and the spring attaching it to the wall will pull it to the right hence k(x1-x2)-kx2 and then I simplified

 

[questionas]

Shouldn't the matrix have 0.5k ... -0.5k in the second row? Is that a typo or that's how you proceed in your original work

I proceeded with 0.5k. I do not understand why it should be negative?

 

[Delta2]

You have the second row as 0.5k k, i think it should be 0.5k -0.5k because the equation for $x_2$ is $$2mx_2''(t)=kx_1-kx_2$$ correct?

 

[questionas]

You have the second row as 0.5k k, i think it should be 0.5k -0.5k because the equation for $x_2$ is $$2mx_2''(t)=kx_1-kx_2$$ correct?

I thought it would be

2mx''(t) = k(x1-x2)-kx2
2mx''(t) = kx1 - 2kx2
mx''(t) = 0.5kx1 - kx2 ?

 

[Delta2]

Ok that's right after all, sorry for that, I solve the final equation from determinant=0 with the help of wolfram and I got the answers given by your book, seems to me you did some error there.

 

[Delta2]

https://www.wolframalpha.com/input?i=solve+(-k+mx^2)(-k+mx^2)-0.5k^2=0

 

[questionas]

https://www.wolframalpha.com/input?i=solve+(-k+mx^2)(-k+mx^2)-0.5k^2=0

Intreasting. I'll try the math again.

 

[questionas]

https://www.wolframalpha.com/input?i=solve+(-k+mx^2)(-k+mx^2)-0.5k^2=0

I figured out what I was doing wrong. I forgot to take the square root of the 0.5 . Silly mistake. Thank you for the help.