Angular momentum conservation help

[snoggerT]

A bola consists of three massive, identical spheres conected to a common point by identical lengths of sturdy string (Fig. 11-51a). To launch this native South American weapon, you hold one of the spheres overhead and then rotate that hand about its wrist so as to rotate the other two spheres in a horizontal path about the hand. Once you manage sufficient rotation, you cast the weapon at a target. Initially the bola rotates around the previously held sphere at angular speed i but then quickly changes so that the spheres rotate around the commonconnection point at angular speed f (Fig. 11-51b).

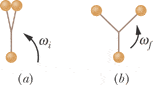
(a) What is the ratio f /i?

(b) What is the ratio Kf /Ki of the corresponding rotational kinetic energies?



Li=Lf

The Attempt at a Solution

- I'm absolutely stumped on this problem. Mainly because I'm given no numbers and don't know how to get a ratio with just the equations. Where would I begin on a problem like this?

 

[learningphysics]

I believe the idea is that the angular momentum about the center of mass is conserved... gravity is the only force acting once the bola is released... and gravity doesn't exerts 0 torque about the center of mass of the system...

given the initial angular speed i... what is the angular momentum about the center of mass initially... you'll have to find the center of mass...

and what's the angular momentum about the center of mass afterwards...

finally set the initial angular momentum = final angular momentum... this will give a relationship between f and i...