qsduahuw
- 1
- 1
- Homework Statement
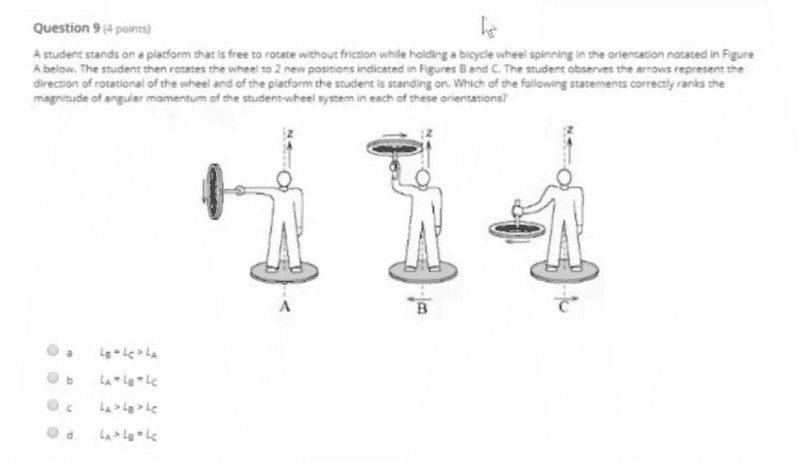
- See image below.
- Relevant Equations
- N/A
I thought the answer is B because the angular momentum in conserved in all 3 pictures.
<Moderator's note: Use of external servers not allowed. Please upload all images to PF.>
<Moderator's note: Use of external servers not allowed. Please upload all images to PF.>
Last edited by a moderator: