Angular velocity of a rod - translational KE?

[Alettix]

Hello! :)

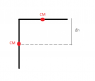
When solving a problem, I had to calculate the angular velocity of a homogenius rod when it comes to vertical position, after being released from a horisontal position (the rod is fixed at one end). This is as usually done with energy conservation, using the rotational energy of the rod and setting it equal to the change in gravitational potential energy. If the length of the rod is L and its mass m, the following is obtained (Δh=L/2):

mL²/3 *ω²/2 = mgL/2
--> ω = (3g/L)^(1/2)

However, I started wondering if this problem could be solved using translational kinetic energy instead. If we consider the center of mass (CM):

mv²/2 = mgL/2
--> v = (Lg)^(1/2)
--> ω = v/(L/2) = 2 (g/L)^(1/2)

As seen, this does not yield the same answer as if we use rotational kinetic energy.
My question is: Why can't translational kinetic energy be used to calculate the angular velocity? or if it can be used: Where am I thinking wrong?

Thank you very much!

 

[copper-head]

Quick question.
How familiar are you with Lagrangian mechanics?

 

[J Hann]

You can use translational energy but would still have to include the rotational energy about the center of mass.
Consider a 2 sticks sliding across ice.
If one was rotating and the other was not rotating then there would have to be a difference in their total energies.

 

[Alettix]

Quick question.
How familiar are you with Lagrangian mechanics?

Not at all unfortunately. I am still high school.

 

[Alettix]

You can use translational energy but would still have to include the rotational energy about the center of mass.
Consider a 2 sticks sliding across ice.
If one was rotating and the other was not rotating then there would have to be a difference in their total energies.

Yes, I understand that there must be a difference between the energy of the two sticks. However, how comes that we never calculate with rotational energy around the pivot point when considering a mass on a thread? What makes the case with the center of mass of the rod different?

 

[J Hann]

You could use rotational energy, but its more straightforward to use translational energy.
m g h = m V^2 / 2 translational KE
m g h = 1/2 I w^2 = 1/2 (m L^2) w^2 = 1/2 m V^2 rotational KE
Same thing.

 

[ehild]

Yes, I understand that there must be a difference between the energy of the two sticks. However, how comes that we never calculate with rotational energy around the pivot point when considering a mass on a thread? What makes the case with the center of mass of the rod different?

The rotational energy of a rod (or any rigid body) is the sum of the translational energies of its tiny pieces.

 

[haruspex]

Why can't translational kinetic energy be used to calculate the angular velocity? or if it can be used:

You can think of the motion of the rod at some instant as the sum of a linear motion of its mass centre plus a rotation about that mass centre. Each contributes to the total KE. Your translational energy assessment lost the rotational energy.
Another way to think about it is to consider ehild's point that the total KE is the sum of all the little KEs. If the KE of a small piece of the rod were proportional to its distance from the axis then reducing it to the motion of the mass centre would work. But its the velocity of a piece that's proportional to the distance from the axis, and as we know, the KE rises as the square of the velocity. So the parts further from the axis carry disproportionately more KE. That puts the effective mass centre (for this purpose) further from the axis, so with a higher velocity than the mass centre.

 

[Alettix]

You can think of the motion of the rod at some instant as the sum of a linear motion of its mass centre plus a rotation about that mass centre. Each contributes to the total KE. Your translational energy assessment lost the rotational energy.
Another way to think about it is to consider ehild's point that the total KE is the sum of all the little KEs. If the KE of a small piece of the rod were proportional to its distance from the axis then reducing it to the motion of the mass centre would work. But its the velocity of a piece that's proportional to the distance from the axis, and as we know, the KE rises as the square of the velocity. So the parts further from the axis carry disproportionately more KE. That puts the effective mass centre (for this purpose) further from the axis, so with a higher velocity than the mass centre.

Thank you very much Sir! This explained a lot!
So, does this also mean that I could use kinetic energy if I integrate v along the rod?

 

[haruspex]

Thank you very much Sir! This explained a lot!
So, does this also mean that I could use kinetic energy if I integrate v along the rod?

If you integrate v² along the rod, yes.

 

[Alettix]

If you integrate v² along the rod, yes.

I tried to do it, but something is wrong. Could you lend me some help, please?

I divide the rod in small segments with mass dm. For a segment at distance r from the pivot point:
dm * rg = dm * v^{^2}/2 (1)
--> v² = 2rg (2)
Now, I don't really know which integration boundaries I should set. I thought that maybe I could get an average speed is I integrated v² from r = 0 to r = L, and divided with L. If I have done it correctly, this yields v^rms = (Lg)^(1/2) . But this can't really be right, because this is the speed at the center of mass, and as previously discussed this doesn't give the right answer.

I also thought that I could rewrite (2) in terms of angular velocity, which gave: ω² = 2g/r . However, something must be wrong here. It looks like the angular velocity is dependent on the distance from the pivot point, but the angular velocity must be constant for all "sections" along the rod!

 

[haruspex]

I tried to do it, but something is wrong. Could you lend me some help, please?

I divide the rod in small segments with mass dm. For a segment at distance r from the pivot point:
dm * rg = dm * v^{^2}/2 (1)

Since v depends on r, you need to make r the integration variable. Replace dm with $\rho dr$ and write v as a function of r.

 

[Alettix]

Since v depends on r, you need to make r the integration variable. Replace dm with $\rho dr$ and write v as a function of r.

But even if $dm = dr \cdot \rho$ , it will cancel out as $dm$ is present on both sides of the equation, won't it?

 

[haruspex]

But even if $dm = dr \cdot \rho$ , it will cancel out as $dm$ is present on both sides of the equation, won't it?

You mean, an r will cancel? No. The rod is rigid. The PE lost by an element does not necessarily provide the KE for that element. This equation:

dm * rg = dm * v^{^2}/2 (1)

is not correct. Only when you integrate both sides does it become correct.

 

[Alettix]

So if $dm = A \rho dr$ where A is the cross-sectional area of the rod:
$\int_{0}^{L} A \rho g r dr = \int_{0}^{L} \frac{A \rho v^2 dr}{2}$
$\frac{gL^2}{2} = \frac{1}{2} \int_{0}^{L} v^2 dr$

Now, $v= r \cdot \omega$ , thus:
$\frac{gL^2}{2} = \frac{\omega^2}{2} \int_{0}^{L} r^2 dr$
which yields $\omega = \sqrt\frac{3g}{L}$
which is the same answer as obtained when using rotational energy.

Thank you very much for your help Sir!

 

[haruspex]

So if $dm = A \rho dr$ where A is the cross-sectional area of the rod:
$\int_{0}^{L} A \rho g r dr = \int_{0}^{L} \frac{A \rho v^2 dr}{2}$
$\frac{gL^2}{2} = \frac{1}{2} \int_{0}^{L} v^2 dr$

Now, $v= r \cdot \omega$ , thus:
$\frac{gL^2}{2} = \frac{\omega^2}{2} \int_{0}^{L} r^2 dr$
which yields $\omega = \sqrt\frac{3g}{L}$
which is the same answer as obtained when using rotational energy.

Thank you very much for your help Sir!

Good stuff.