- #1
rabbahs
- 16
- 0
Hi,
I have some experimental data and I am interested to use this data to calculated modulus of elasticiy (young's modulus) and Poisson's ratio. The material for which the data is given in an anisotropic material, therefore I need to calculate modulus of elasticity and poisson's ration is x,y and z direction.
the data which is have is the stress in three direction and corresponding strain three direction.
So , my problem is simple.
Knows: sigma_x, sigma_y, sigma_z, epsilon_x, epsilon_y, epsilon_y (6 knows)
Unknows: Ex, Ey, Ez, Vxy, Vyx, Vxz (6 unknows).
I have seen a formula in rock mechanics book (see the following image), but it will resolve into only three equation if the share stress is ignored.
Please help me out.
Thanks
Syed
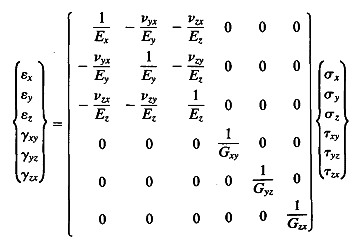
I have some experimental data and I am interested to use this data to calculated modulus of elasticiy (young's modulus) and Poisson's ratio. The material for which the data is given in an anisotropic material, therefore I need to calculate modulus of elasticity and poisson's ration is x,y and z direction.
the data which is have is the stress in three direction and corresponding strain three direction.
So , my problem is simple.
Knows: sigma_x, sigma_y, sigma_z, epsilon_x, epsilon_y, epsilon_y (6 knows)
Unknows: Ex, Ey, Ez, Vxy, Vyx, Vxz (6 unknows).
I have seen a formula in rock mechanics book (see the following image), but it will resolve into only three equation if the share stress is ignored.
Please help me out.
Thanks
Syed