jim hardy
Science Advisor
Homework Helper
Dearly Missed
- 9,832
- 4,898
Whew --- had to take some time off. All internet and no sawdust makes james a dull boy. And my alleged thinker is sooo slow these days...I worked through Baluncor's algebra, for purpose of understanding it and getting my gears synchronized with it.
Of course it is impeccable.
Our models are actually pretty doggone close to equivalent.
I did notice one thing about the posit though.
I plugged turns ratio n into balun's formulas for current and put results on the diagram.
I = V/r * (1/3) * (3/2)
that's 1/2 V/r
drawing those into the diagram is really interesting
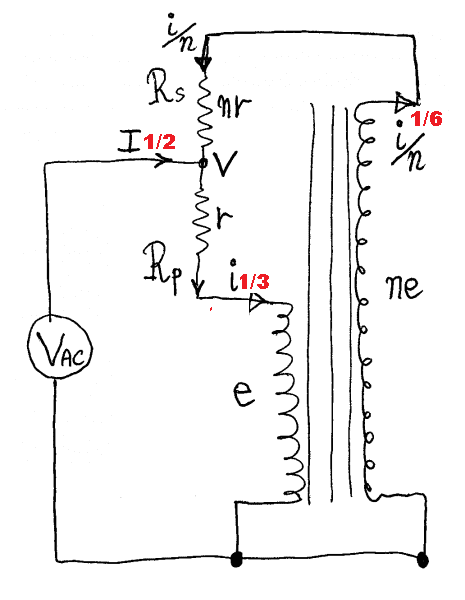
each red number of course multiplied by V/r.
To satisfy Kirchoff's current law current must be same direction in both secondaries not opposite (as was most logically assumed)
because at node V, current entering must equal current leaving and 1/2 + 1/6 = 2/3 not 1/3.
Now it's pretty obvious that'd be the case were e=0. Is there any other e that'd satisfy? I haven't mustered the courage to tackle the frustration of my clumsy algebra to see.
But it's interesting he got the same current ratio in his ideal transformer as i did in my inductor.
Also interesting that he got magnitudes half mine, 1/6 and 2/6 vs my 1/3 and 2/3. Of course i assumed 1 for my I vs his 1/2 probably its that simple.
That shorting turns cancels flux, driving it toward zero, goes along with what the algebra says, current magnitude depends on resistance of windings and how it divides depends on turns ratio.. At zero flux e=0 and our models both give same result there.
Now i'll point out something about ideal transformers.
They take no magnetizing current.
That's why a model of a real transformer has a parallel branch Xm to account for magnetizing current.
That transformers do require magnetizing current is why Iprimary/ Isecondary isn't exactly equal to turns ratio, the currents differ by magnetizing current which is intentionally kept small.
So we must bear in mind that accepting an ideal transformer requires a mental leap
since it requires no magnetizing current
the presence of induction requires zero reluctance
flux = (zero amp-turns)/(zero reluctance), undefined, yet flux in a real transformer is defined.
that means infinite permeability , and some magnetic alloys do have so much permeability that for sliderule accuracy you can get away with calling it infinite. And we do often ignore magnetizing current.
That's what i was trying to allow for with my jΦ term.
@Baluncore core I hope this wasn't taken as criticism at all !
Instead i celebrate having learned something, and i really enjoy sharing interests with folks..In that guy's transformer i'd add a third winding with fifty amp turns .
When i get something going that'll run Basic i'll be able to tinker with core reluctance, winding resistances, and a secondary side load resistance.
But that's a few projects away.
old jim
Of course it is impeccable.
Our models are actually pretty doggone close to equivalent.
I did notice one thing about the posit though.
I plugged turns ratio n into balun's formulas for current and put results on the diagram.
okay primary i = V/r * (2-1) / (2+1) = 1/3 V/rBaluncore said:i = ( V / r ) * ( ( n – 1 ) / ( n + 1 ) )
That's 1/3 divided by 2 = 1/6 V/rBaluncore said:The secondary current is, i / n.
I = V/r * * (2-1)/(2+1) * (1+1/2)Baluncore said:Knowing i = I + i/n, solve for driving current I = i – i/n
I = ( V / r ) * ( ( n – 1 ) / ( n + 1 ) ) * ( 1 + 1/n )
I = V/r * (1/3) * (3/2)
that's 1/2 V/r
drawing those into the diagram is really interesting
each red number of course multiplied by V/r.
To satisfy Kirchoff's current law current must be same direction in both secondaries not opposite (as was most logically assumed)
because at node V, current entering must equal current leaving and 1/2 + 1/6 = 2/3 not 1/3.
Now it's pretty obvious that'd be the case were e=0. Is there any other e that'd satisfy? I haven't mustered the courage to tackle the frustration of my clumsy algebra to see.
But it's interesting he got the same current ratio in his ideal transformer as i did in my inductor.
Also interesting that he got magnitudes half mine, 1/6 and 2/6 vs my 1/3 and 2/3. Of course i assumed 1 for my I vs his 1/2 probably its that simple.
That shorting turns cancels flux, driving it toward zero, goes along with what the algebra says, current magnitude depends on resistance of windings and how it divides depends on turns ratio.. At zero flux e=0 and our models both give same result there.
Now i'll point out something about ideal transformers.
They take no magnetizing current.
That's why a model of a real transformer has a parallel branch Xm to account for magnetizing current.
That transformers do require magnetizing current is why Iprimary/ Isecondary isn't exactly equal to turns ratio, the currents differ by magnetizing current which is intentionally kept small.
So we must bear in mind that accepting an ideal transformer requires a mental leap
since it requires no magnetizing current
the presence of induction requires zero reluctance
flux = (zero amp-turns)/(zero reluctance), undefined, yet flux in a real transformer is defined.
that means infinite permeability , and some magnetic alloys do have so much permeability that for sliderule accuracy you can get away with calling it infinite. And we do often ignore magnetizing current.
That's what i was trying to allow for with my jΦ term.
( Actually I'm trying to build a mental model for myself to understand CT's with parallel secondaries of unequal turns like that guy asked us about in https://www.physicsforums.com/threads/how-many-turns-on-a-50-5-ct.586722/
)tinkeringone said:Thanks, Jim. I followed your advice, and dissected it, and saw a spot where the windings had arced across at least a couple of turns. As far as the number of turns go, it has 2 parallel wires wound around the core. I counted 19 wire turns around the core. And that's because one of the 2 parallel wires is 25" long from terminal to terminal, and the other is only 22" long. The 25" long wire had 10 turns around the core, and the 22" one had only 9 turns - it wasn't long enough for them to make the 10th turn.
The 2 parallel wires are each 0.038" in diameter, like maybe 19 gauge? I'm wondering if I could just run 9 or 10 turns of a single, 16 gauge wire, instead of paralleling 2 smaller ones like they did. But I'm wondering if they had a good reason for paralleling those 2 smaller wires. I mean it does seem like you'd be spreading out the winding a bit more by doing that. That parallel setup spanned about 3/4 of the core circumference.
Anyhow
i'd like to try baluncore's algebra with a magnetizing branch added, and induced voltage as ideal sources controlled by magnetizing current.
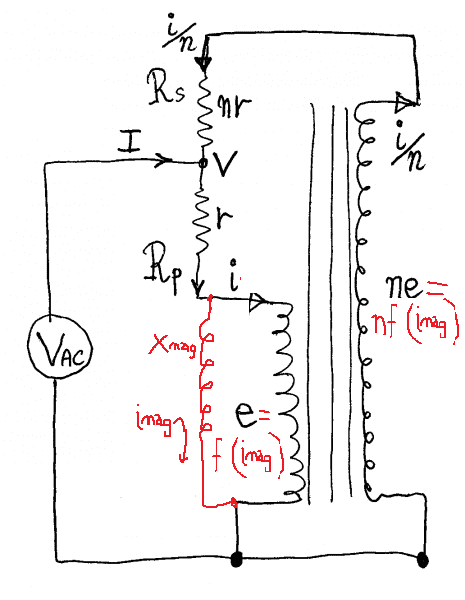
Sigh. That's an early morning sort of thing.
i'd like to try baluncore's algebra with a magnetizing branch added, and induced voltage as ideal sources controlled by magnetizing current.
Sigh. That's an early morning sort of thing.
@Baluncore core I hope this wasn't taken as criticism at all !
Instead i celebrate having learned something, and i really enjoy sharing interests with folks..In that guy's transformer i'd add a third winding with fifty amp turns .
When i get something going that'll run Basic i'll be able to tinker with core reluctance, winding resistances, and a secondary side load resistance.
But that's a few projects away.
old jim
Last edited:







