Answer Check: Displacement Currents and Capacitors

[TFM]

Homework Statement

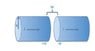
A fat wire, radius a, carries a constant current I, uniformly distributed over its cross section. A narrow gap in the wire, of width w << a, forms a parallel-plate capacitor, as shown in the figure above. Find the magnetic field in the gap, at a distance s < a from the axis.

{Figure given below}

Homework Equations

displacement current, J_d = \epsilon_0 \frac{\partial E}{\partial t} --- (1)

\frac{\partial E}{\partial t} = \frac{1}{\epsilon_0 A}I --- (2)

B(r) = \frac{\mu_0 I}{2 \pi r} --- (3)

The Attempt at a Solution

Okay so firstly, I have put together (1) and (2) to get:


J_d = \epsilon_0 \frac{1}{\epsilon_0 A}I

I got this to cancel down into:

J_d = \frac{I}{A}

I then made a very bold assumption that the current in B(r) = the displacement current J_d

So I Inserted the values and got:

B(r) = \frac{\mu_0 \left( \frac{I}{A}\right)}{2 \pi r}

This seems very quick and straight forwards, though...

Does this look correct?

TFM

 

[TFM]

Does this look right?