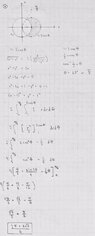MHB ANSWER CHECK: Double Integral in Polar

Pull and Twist
Messages
48
Reaction score
0
Here is the problem I am dealing with...
View attachment 6027

And this is how I approached it. Can anyone confirm that I did it correctly and got the right answer?

View attachment 6028

Thank you.
 

Attachments

  • image.jpeg
    image.jpeg
    6.7 KB · Views: 80
  • image.jpeg
    image.jpeg
    31.9 KB · Views: 87
Physics news on Phys.org
PullandTwist said:
Can anyone confirm that I did it correctly and got the right answer?
Yes, it's all good. (Yes)
 
Thank you for verifying it for me. 🙂
 

Similar threads

A Double integral with infinite limits
Replies
11
Views
3K
MHB Double Integrals in Polar Coordinates
Replies
4
Views
2K
MHB Double Integrals in Polar Coordinates
Replies
6
Views
3K
I How to evaluate the enclosed area of this implicit curve?
Replies
2
Views
3K
I Did Math DF's integral calculator make a glaring mistake?
Replies
8
Views
3K
MHB How to Find the Surface Area of a Pringle Using Double Integration?
Replies
1
Views
2K
I How to Approach a Double Exponential Integral?
Replies
3
Views
2K
MHB ANSWER CHECK: Sum of Double Integrals involving Polar Conversion
Replies
2
Views
1K
I Q about finding area with double/volume with triple integral
Replies
4
Views
2K
B Question about the limits of integration in a change of variables
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top