- #1
CornMuffin
- 55
- 5
The Apollonian Packing is generated by starting out with 3 mutually tangent circle and then using descartes theorem to find two other circles that are mutually tangent to each other. This creates 6 curvilinear triangles, and in each, we inscribe a circle tangent to all three of the sides that formed the curvilinear triangle. And we do this for each of the newly formed curvilinear triangles, so the Apollonian Packing looks like this:
Descartes circle theorem states: Given four circles with mutual extermal contact with curvature
And here is an example
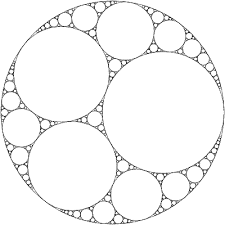
But the one problem that I am having is how do I calculate the center of any of the circles in the Apollonian Packing of Circles
Descartes circle theorem states: Given four circles with mutual extermal contact with curvature
And here is an example
But the one problem that I am having is how do I calculate the center of any of the circles in the Apollonian Packing of Circles