Apparent depth of an object underwater

[lorenz0]

Homework Statement

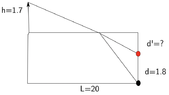
A person (the arrow at the upper left of the figure) of height $h=1.7m$ is standing at the edge of a pool of water of depth $d=1.8m$ in which there is an object located at the farthest end of the pool (black ball in the figure). What is the apparent depth of this object for the person looking at the pool, i.e. what is the depth of the object observed by the person (red ball in the figure)?

Relevant Equations

$n_1 \sin(\theta_1)=n_2\sin(\theta_2)$

I would know how to solve this problem if the person had been standing pratically above of the object underwater by using Snell's law and the approximation $\sin(\theta)\approx\tan(\theta)$ fopr $\theta$ small, but in this case I don't see how to find the angles $\theta_1$ and $\theta_2$ and, above all, at what point along the surface of the water the light with come out in such a way as to reach the eye of the person. Without this last information, when I try to set up Snell's law I get (with $x$ representing the distance from the left corner at which the light comes out): $\frac{d^2+(L-x)^2}{d'^2+(L-x)^2}=1.33^2$ but I have too many variables.

So, I would appreciate if someone could point me twoards a viable strategy to solve this problem. Thanks

 

[haruspex]

Find the two angles as functions of x.

 

[lorenz0]

Find the two angles as functions of x.

Thanks. I got $x\approx 18\ m$ and an apparent depth of $d'\approx 0.19\ m$.

 

[haruspex]

Thanks. I got $x\approx 18\ m$ and an apparent depth of $d'\approx 0.19\ m$.

That looks right.