- #1
czmat
Hi,
I've got a question regarding application of the Biot-savart law along finite wire.
There is a great explenation of this problem in the MIT paper but this does not cover one case.
1. Homework Statement
My question is: does the equation defining magnetic field in point P(x,y) also applies to the point P_1(x,y) (as in the picture below) which is not in boundaries of the wire?
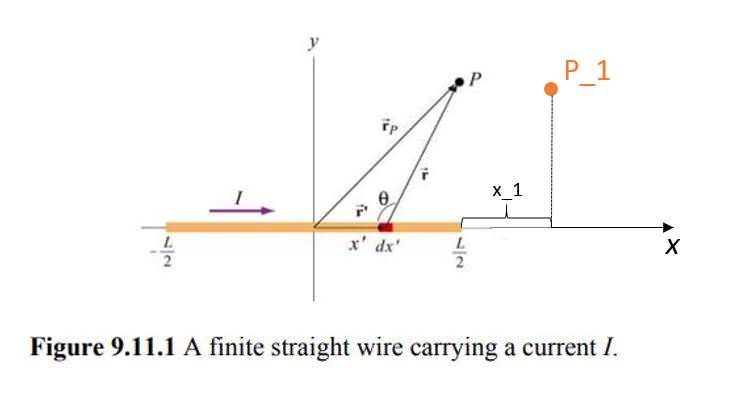
Magnetic field in point P(x,y) (as in the above figure) along finite wire is:
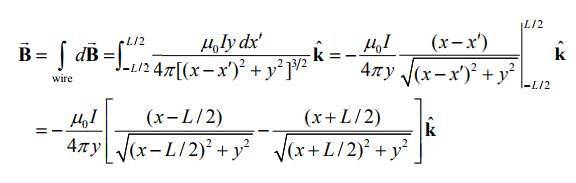
My guess is: yes, just because I can put P_1 coordinates in the equation, but intuition tells me that I am omitting something and unfortunately I don't know what.
I've got a question regarding application of the Biot-savart law along finite wire.
There is a great explenation of this problem in the MIT paper but this does not cover one case.
1. Homework Statement
My question is: does the equation defining magnetic field in point P(x,y) also applies to the point P_1(x,y) (as in the picture below) which is not in boundaries of the wire?
Homework Equations
Magnetic field in point P(x,y) (as in the above figure) along finite wire is:
The Attempt at a Solution
My guess is: yes, just because I can put P_1 coordinates in the equation, but intuition tells me that I am omitting something and unfortunately I don't know what.