Application of Differentiation - Points of Inflection.

[Nemo1]

Hi Community,

I have this question.

View attachment 5067

When I graph it I get:

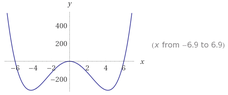
View attachment 5064

When I answer the first sets of questions

a,

Intercepts: $$x=(-6), x=0, x=6$$

Stationary points: $$(0,0) , (-3\sqrt{2}, -324) , (3\sqrt{2}, -324)$$

Points of inflection: $$ x=0 $$ This is where I was wrong. (It's a turning point isn't it?)

How do I work out the points of inflection?

I realized now there should be two at around $$(-3ish,-200ish)$$ & $$(3ish,-200ish)$$
(Could be more, as I am still trying to learn where a point of inflection is and isn't)

b, State where the function $$x^4-36^2$$ is:

Non negative: $$(-6,0) , (6,0) , (0,0)$$

Increasing: $$(-3 \sqrt{2}, -324)$$ $$\to$$ $$(0,0)$$ then $$(3 \sqrt{2}, -324) $$ $$\to$$ $$(\infty,\infty)$$

Concave up: $$(-\infty,0]$$ & $$[0,\infty)$$

Please review all of my answers and point out if there is a better way to express them more accurately.

Many thanks for your time in advance.

Cheers

Nemo.

(Not sure why the attached imaged are there, can't find where to delete them either sorry)

 

[MarkFL]

Hello Nemo!

I edited your post and deleted the duplicate images, leaving only the ones attached inline. :)

Okay...we are given the function:

$$y(x)=x^4-36x^2$$

This first thing I notice about this function is that it's even, that is $y(-x)=y(x)$, which means all behaviors will be "mirrored" across the $y$-axis, so we really need only concern ourselves with non-negative values of $x$, and the refelct across the $y$-axis when it is convenient to do so.

On to the questions...

Intercepts:

To find the $y$-intercept, we set $x=0$, and so it will be at $\left(0,y(0)\right)=(0,0)$.

To find the $x$-intercept(s), we set $y=0$ and solve for $x$:

$$y(x)=x^4-36x^2=x^2\left(x^2-6^2\right)=x^2(x+6)(x-6)=0$$

And so we see that the $x$-intercepts are (by equating each factor in turn to zero):

$$(-6,0),\,(0,0),\,(6,0)$$

Stationary points:

These are points where the first derivative is zero...so let's see:

$$y'(x)=4x^3-72x=4x\left(x^2-18\right)=4x(x+3\sqrt{2})(x-3\sqrt{2})=0$$

$$y(0)=0$$

$$y(3\sqrt{2})=18^2-36(18)=-18^2=-324$$

And so the stationary points are: $$(0,0),\,\left(\pm3\sqrt{2},-324\right)$$

Points of inflection:

These are where the second derivative is zero AND the concavity changes across these points, that is, the sign of the second derivative changes.

$$y''(x)=12x^2-72=12\left(x^2-6\right)=12(x+\sqrt{6})(x-\sqrt{6})=0$$

We see each root is of odd multiplicity (they occur once, and 1 is an odd number), and so we know the sign of $y''$ will alternate across each root, and so we find:

$$y\left(\pm\sqrt{6}\right)=6^2-6^3=6^2(1-6)=-180$$

And thus, the points of inflection are at:

$$\left(\pm\sqrt{6},-180\right)$$

Non-negative:

$$y(x)\ge0$$

$$x^4-36x^2\ge0$$

$$x^2(x+6)(x-6)\ge0$$

We observe that the root $x=0$ is of even multiplicity, and so the sign of $y$ will not change across this root. We see that the sign of the term with the largest exponent is positive, and this exponent is even, and so we know:

$$\lim_{x\to\pm\infty}=\infty$$

and so we may conclude that $y$ is non-negative on:

$$(-\infty,-6)\,\cup\,[0,0]\,\cup\,(6,\infty)$$

Increasing:

These are in intervals where the first derivative is positive:

$$y'(x)=4x^3-72x=4x\left(x^2-18\right)=4x(x+3\sqrt{2})(x-3\sqrt{2})>0$$

We see that:

$$\lim_{x\to\pm\infty}=\pm\infty$$

and that all roots of $y'$ are of odd multiplicity, and so we may conclude that in the 4 intervals made by the 3 roots, we will have decreasing/increasing/decreasing/increasing, so we know the function is increasin on the 2nd and 4th intervals, given by:

$$\left(-3\sqrt{2},0\right)\,\cup\,(3\sqrt{2},\infty)$$

Concave up:

These are the intervals where the second derivative is positive:

$$y''(x)=12x^2-72=12\left(x^2-6\right)=12(x+\sqrt{6})(x-\sqrt{6})>0$$

We see that $y''$ is a parabola opening upwards, and so we know that over the 3 intervals created by the 2 roots, the sign will alternate positive/negative/positive from left to right. And so we conclude that $y$ is concave up on:

$$(-\infty,-\sqrt{6})\,\cup\,(\sqrt{6},\infty)$$

 

[Nemo1]

Hi Mark,

Thanks for the detailed explanation,

I am unsure of how you went from:

$$y''(x)=12x^2-72=12\left(x^2-6\right)=12(x+\sqrt{6})(x-\sqrt{6})=0$$

to:

$$y\left(\pm\sqrt{6}\right)=6^2-6^3=6^2(1-6)=-180$$

to:

$$\left(\pm\sqrt{6},-180\right)$$

Can you please break this down for me.

Also when you said:

We see each root is of odd multiplicity (they occur once, and 1 is an odd number), and so we know the sign of $y''$ will alternate across each root, and so we find:

Is this because the sign on the $y$ axis change from positive to negative when $$x=\pm6$$

Cheers Nemo

 

[MarkFL]

I am unsure of how you went from:

$$y''(x)=12x^2-72=12\left(x^2-6\right)=12(x+\sqrt{6})(x-\sqrt{6})=0$$

to:

$$y\left(\pm\sqrt{6}\right)=6^2-6^3=6^2(1-6)=-180$$

to:

$$\left(\pm\sqrt{6},-180\right)$$

Can you please break this down for me.

We see that the roots of $y''$ are $x=\pm\sqrt{6}$, and so these are the $x$-values at which the points of inflection will occur. So we need to evaluate $y$ at these values:

$$y(\pm\sqrt{6})=(\pm\sqrt{6})^4-36(\pm\sqrt{6})^2=6^2-6^2(6)=6^2-6^3=6^2(1-6)=36(-5)=-180$$

And so the two inflection points are $(-\sqrt{6},-180)$ and $(\sqrt{6},-180)$, which we may more concisely state as:

$$(\pm\sqrt{6},-180)$$

Also when you said:

We see each root is of odd multiplicity (they occur once, and 1 is an odd number), and so we know the sign of $y''$ will alternate across each root, and so we find:

Is this because the sign on the $y$ axis change from positive to negative when $$x=\pm6$$

There, I was making use of the fact that when a function has a root of odd multiplicity, the function's graph will pass through the $x$-axis. When there is a root of even multiplicity, then the function will be tangent to the $x$-axis, and not pass through it.

If a function has only roots of odd multiplicity, then the sign of that function will alternate across all of its roots. Consider the simple case of:

$$f(x)=x$$

It has the root $x=0$ and it is of multiplicity 1, and we see that the function goes from negative to positive as it crosses this root. Its sign has changed. Then look at the function:

$$g(x)=x^2$$

It has the root $x=0$ and it is of multiplicity 2, and we see that the function goes from positive to positive as it crosses this root. Its sign has not changed.

This holds true for functions having multiple roots. Look at the graph of $y=(x-1)(x-2)$:

View attachment 5070

Observe how the function changes sign across both roots. Now look at the graph of $y=(x-1)(x-2)^2$

View attachment 5071

See how the function changes sign across the root of odd multiplicity ($x=1$), but does not change sign across the root of even multiplicity ($x=2$).

Making use of the parity (whether it is odd or even) of the multiplicity of roots allows you to easily find the sign of a function across all intervals once you establish the sign in just one interval. This way you do not need to tediously test a point in each interval.

 

[Ackbach]

Another way you can show that a candidate point of inflection actually is a point of inflection is to show that the point satisfies these criteria: $f''(a)=0$, AND $f'''(a)\not=0$ (or the lowest non-zero derivative above the second derivative has to be of odd order). This ensures that the concavity will actually change at $a$.

 

[Nemo1]

Thanks Mark and Ackbach,

I had myself in a tail spin till I took a break and came back to it and realized that in Mark's explanation of the point of inflection we are plugging the $$\pm\sqrt{6}$$ back into the original equation $$y=x^4-36x^2$$.

Many many thanks for everyones time in clarifying this for me.

Cheers Nemo