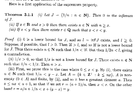Application of Supremum Property .... Garling, Theorem 3.1.1 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume I: Foundations and Elementary Real Analysis ... ...

I am focused on Chapter 3: Convergent Sequences

I need some help to fully understand the proof of Theorem 3.1.1 ...Garling's statement and proof of Theorem 3.1.1 (together with some interesting remarks) reads as follows:
View attachment 9026
View attachment 9027
In the above text by Garling, in the proof of statement (iii), we read the following:

" ... ... Let \(\displaystyle A = \{ k \in \mathbb{Z}^{ + } \ : \ k \leq nx \}\). A is non-empty ( \(\displaystyle 0 \in A\) ) and finite, by (ii) ... ... " My question is as follows:

Although it is plausible (maybe even "obvious" ... ) that A is finite ... how do we logically and rigorously prove this using (ii} ... that is, logically and rigorously, how does (ii) imply that A is finite ...?

Help will be appreciated ... ...

Peter

 

[jvicens]

Hello Peter,

Thank you for reaching out for help with understanding the proof of Theorem 3.1.1 in Garling's book. I can see why you are having trouble understanding the implication of (ii) in proving that A is finite. Let me try to explain it in a more detailed and step-by-step manner.

First, let's recall what statement (ii) in the theorem states:

(ii) If A is a non-empty subset of \mathbb{Z}^{ + } such that A is bounded above, then A has a maximum element.

Now, let's look at the set A defined in the proof of statement (iii):

A = \{ k \in \mathbb{Z}^{ + } \ : \ k \leq nx \}

From this definition, we can see that A is a subset of \mathbb{Z}^{ + }, the set of positive integers. Also, A is bounded above by nx, since all elements in A are less than or equal to nx. Therefore, according to (ii), A has a maximum element, say m. This means that m is the largest element in A, and any other element in A is less than or equal to m.

Now, let's consider the set B = \{ k \in \mathbb{Z}^{ + } \ : \ k \leq (n+1)x \}. This set is also bounded above by (n+1)x, and according to (ii), it has a maximum element, say m'. Similar to m, m' is the largest element in B, and any other element in B is less than or equal to m'.

But notice that A is a subset of B, because any element in A is also in B (since A is defined as the set of all positive integers less than or equal to nx, and B is defined as the set of all positive integers less than or equal to (n+1)x). Therefore, m' is also an upper bound for A, and since m is the maximum element of A, we must have m' \geq m.

However, this means that m' is also an element of A, since m' is the largest element in B, and any other element in B is less than or equal to m'. But this contradicts the fact that m is the maximum element of A. Therefore, our assumption that m' is an element of A