Apply DFS to Minimize Antennas on Road

[evinda]

Hello! (Wave)

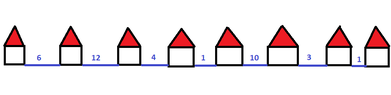
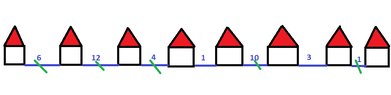
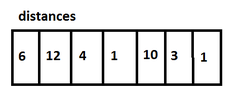
We consider a long straight road along of which there are some houses.
A mobile phone company wants to put antennas along the road for the service of the residents of the homes.
The range of each antenna is four kilometers.
Give an algorithm that puts the smallest number of antennas.Could we consider the road as edges and the houses as vertices?
If so, then could we maybe apply DFS and mark the 4th edge, then the 8th and so on? (Thinking)

 

[Nono713]

I don't see how a graph formulation (or DFS) is useful here, especially given the "graph" is pretty simple, it's just a straight line with houses at regular intervals. So you can do it with a much simpler algorithm, assuming I understand the problem correctly, where the houses are assumed to be "on" the road at arbitrary positions.

I would begin by placing an antenna as far as possible along the road so that the first house is in range of it. Then, find the next closest house that is not in range of that antenna, and repeat. This can be done by simply sorting the houses by their distance along the road. The key to prove that this is optimal is to observe that the range of the antennas can overlap if needed (I assume) and that therefore the algorithm makes the optimal choice at each step because any other choice would either miss a house (requiring an additional antenna) or waste space (which means it can't be a better choice). Or at least I think...

 

[evinda]

I don't see how a graph formulation (or DFS) is useful here, especially given the "graph" is pretty simple, it's just a straight line with houses at regular intervals. So you can do it with a much simpler algorithm, assuming I understand the problem correctly, where the houses are assumed to be "on" the road at arbitrary positions.

I would begin by placing an antenna as far as possible along the road so that the first house is in range of it. Then, find the next closest house that is not in range of that antenna, and repeat.

So will we have for example such a straight line with houses?

View attachment 4355

If so, then would we put an antenna at the following green marked positions?

View attachment 4356

This can be done by simply sorting the houses by their distance along the road.

What do you mean with the fact that we could simply sort the houses by their distance along the road?
Do we check if the distance between two houses is less or equal to $4$? Or have I understood it wrong? (Worried)

The key to prove that this is optimal is to observe that the range of the antennas can overlap if needed (I assume) and that therefore the algorithm makes the optimal choice at each step because any other choice would either miss a house (requiring an additional antenna) or waste space (which means it can't be a better choice). Or at least I think...

Could you explain me further why this is optimal? I haven't understood it...

 

[I like Serena]

Hey! (Wave)

If so, then would we put an antenna at the following green marked positions?

View attachment 4356

The antenna in the 12 km section will cover either no house at all, or only 1 house.
So this is not a useful antenna. (Worried)Since each house has to be covered, we can start with the first house and put an antenna 4 km beyond it.
This choice has the most possible benefit and an antenna will be required within 4 km of the house. (Thinking)

Then we can find the next house that is not covered yet and repeat the procedure.

We are free to shift the antennas backward a bit as long as they still cover the same houses.When we're finished we'll have a solution with a minimal number of antennas.
There can be other solutions, for instance if we start at the other end of the road, but since it will also be optimal, it will have the same number of antennas. (Mmm)

 

[evinda]

Hey! (Wave)
The antenna in the 12 km section will cover either no house at all, or only 1 house.
So this is not a useful antenna. (Worried)Since each house has to be covered, we can start with the first house and put an antenna 4 km beyond it.
This choice has the most possible benefit and an antenna will be required within 4 km of the house. (Thinking)

Then we can find the next house that is not covered yet and repeat the procedure.

We are free to shift the antennas backward a bit as long as they still cover the same houses.When we're finished we'll have a solution with a minimal number of antennas.
There can be other solutions, for instance if we start at the other end of the road, but since it will also be optimal, it will have the same number of antennas. (Mmm)

Do we have to create a struct that contains the number of the house and its distance from the next one? (Thinking)

Also do we have to count the sum of the distances $s$ and then create an array $A$, initialize all of its positions $A[1], A[2], \dots, A$ with $0$, compare the distance of the first house from the second one and set an appropriate value $A$ equal to $1$ and so on?

For example, in our road the distance of the first house to the second one is $6$. So would we have to set $A[2]$ or $A[3]$ equal to $1$?
Then the distance of the second house from the third one is $12$. So do we have to set $A[6+4]$ and $A[6+12-4]$ equal to $1$? (Thinking)

 

[I like Serena]

Do we have to create a struct that contains the number of the house and its distance from the next one? (Thinking)

Also do we have to count the sum of the distances $s$ and then create an array $A$, initialize all of its positions $A[1], A[2], \dots, A$ with $0$, compare the distance of the first house from the second one and set an appropriate value $A$ equal to $1$ and so on?

For example, in our road the distance of the first house to the second one is $6$. So would we have to set $A[2]$ or $A[3]$ equal to $1$?
Then the distance of the second house from the third one is $12$. So do we have to set $A[6+4]$ and $A[6+12-4]$ equal to $1$? (Thinking)

There doesn't really seem to be a need to keep structures for this problem. (Thinking)

I suggest to iterate over the input (distances between the houses), track the total distance, and track the distance from the first house that is not covered yet.
Then output the appropriate antenna locations and the total number of antennas. (Sweating)

 

[evinda]

There doesn't really seem to be a need to keep structures for this problem. (Thinking)

I suggest to iterate over the input (distances between the houses), track the total distance, and track the distance from the first house that is not covered yet.
Then output the appropriate antenna locations and the total number of antennas. (Sweating)

In our example, the input is the following, right?

View attachment 4358

We can place an antenna at the 4th kilometer, then at the (6+12)th kilometer, and then we don't have to put an other antenna for the next house. Then we put an antenna at the (6+12+4+2+1)th kilometer, then at the (6+12+4+2+1+10)th kilometer and then we are done.
Or have I understood it wrong? (Thinking)

 

[I like Serena]

In our example, the input is the following, right?
We can place an antenna at the 4th kilometer, then at the (6+12)th kilometer, and then we don't have to put an other antenna for the next house. Then we put an antenna at the (6+12+4+2+1)th kilometer, then at the (6+12+4+2+1+10)th kilometer and then we are done.
Or have I understood it wrong? (Thinking)

First antenna should indeed be at 0+4=4, but the second should be at 6+12+4, covering 3 houses instead of 2.
Each antenna goes 4 km beyond the first house that is not covered yet. (Wasntme)

 

[evinda]

First antenna should indeed be at 0+4=4, but the second should be at 6+12+4, covering 3 houses instead of 2.
Each antenna goes 4 km beyond the first house that is not covered yet. (Wasntme)

So should the algorithm look as follows?

Algorithm(distances[0...n-1]){
  number=0;
  km=0;
  for (i=0; i<n-1; i++){
        km=km+4;
        number++;
        printf("%d",km);
        km=km+distance[i]+distance[i+1];
  }
}

 

[I like Serena]

So should the algorithm look as follows?

What would the result be on your example input? (Wondering)

 

[evinda]

What would the result be on your example input? (Wondering)

For [m] i=0 [/m] the algorithm prints [m] 4 [/m].
For [m] i=1 [/m] it prints [m] 4+6+12+4 [/m] and this is wrong.

So the mistake should be at this command: [m] km=km+distance+distance[i+1] [/m], right? (Thinking)

 

[I like Serena]

For [m] i=0 [/m] the algorithm prints [m] 4 [/m].
For [m] i=1 [/m] it prints [m] 4+6+12+4 [/m] and this is wrong.

So the mistake should be at this command: [m] km=km+distance+distance[i+1] [/m], right? (Thinking)

Indeed, there seems to be some assumption in there. (Wasntme)
What is the command supposed to do? (Wondering)

 

[evinda]

Indeed, there seems to be some assumption in there. (Wasntme)
What is the command supposed to do? (Wondering)

I am a little confused now.. Is it right as follows?

Distance of first from second house: 6 ---> We put an antenna at 4th kilometer so both of the houses have access to the antenna.

Distance of second from third house: 12 ---> The second house has already access so we have to put an antenna at the (6+12+4)th kilometer.

Distance of third from 4th house: 4 ---> The third house has already access so we have to put an antenna at the (6+12+4+4)th kilometer.

Distance of 4th from 5th house: 1 ---> The 4th house has already access so we have to put an antenna at the (6+12+4+1+4)th kilometer.If it is like that, then the formula for the kilometers, except from the first one that is 4, is the following:

$$km=\sum_{i=0}^j \text{distance}+4$$

when we are looking at the $j-$th house.

Or am I wrong? (Thinking)

 

[I like Serena]

It should be like this:
$$\newcommand{\house}{\stackrel{\color{red}{\blacktriangle}}{\Box}}
\newcommand{\antenna}{\maltese}

\underbrace{\house 6 \house}_{\underset 4\antenna}\ 12\ \underbrace{\house 4 \house 1 \house }_{\underset {(6+12)+4}\antenna}\ 10\ \underbrace{\house 3 \house 1 \house}_{\underset {(6+12+4+1+10)+4}{\qquad\quad\antenna}}
$$
(Wasntme)

 

[evinda]

It should be like this:
$$\newcommand{\house}{\stackrel{\color{red}{\blacktriangle}}{\Box}}
\newcommand{\antenna}{\maltese}

\underbrace{\house 6 \house}_{\underset 4\antenna}\ 12\ \underbrace{\house 4 \house 1 \house }_{\underset {(6+12)+4}\antenna}\ 10\ \underbrace{\house 3 \house 1 \house}_{\underset {(6+12+4+1+10)+4}{\qquad\quad\antenna}}
$$
(Wasntme)

Is this algorithm right? Algorithm(distance[0...n-1]){ dist[0]=0 // dist is the distance of the fi - Pastebin.com

 

[I like Serena]

Is this algorithm right? Algorithm(distance[0...n-1]){ dist[0]=0 // dist is the distance of the fi - Pastebin.com

What would be its output for the example? (Wondering)

 

[evinda]

What would be its output for the example? (Wondering)

It wasn't right, so I edited my previous post.. No I get the right result.. Do you agree with the algorithm? (Thinking)

 

[I like Serena]

It wasn't right, so I edited my previous post.. No I get the right result.. Do you agree with the algorithm? (Thinking)

The algorithm looks fine to me. (Happy)
As far as I can tell the important parts (2 nested loops) are in place, including checks for termination and edge cases.
I didn't check if it will actually do the job, or if all edge cases are covered properly. (Tauri)