Applying the Work-Energy theorem to a system

[sachin]

Homework Statement

I am trying to solve the given question based on energy conservation,but am stuck with the analysis of the equations.

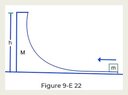
The question says find the velocity of the bigger block when the smaller block initially given a velocity v and sliding on the horizontal part of the bigger block reaches the top of the bigger block of height h.All surfaces are frictionless.

Relevant Equations

using conservation of energy,
we get 1/2 mv2 = 1/2 mvx2 + 1/2 mvy2 + 1/2 Mvx2,where vx is the common horizontal velocity of the blocks and vy the verical velocity of the smaller block when it reaches the top of the bigger block.

I am trying to solve the given question based on energy conservation,but am stuck with the analysis of the equations.

The question says find the velocity of the bigger block when the smaller block initially given a velocity v and sliding on the horizontal part of the bigger block reaches the top of the bigger block of height h.All surfaces are frictionless.

using conservation of energy,
we get 1/2 mv2 = 1/2 mvx2 + 1/2 mvy2 + 1/2 Mvx2,where vx is the common horizontal velocity of the blocks and vy the verical velocity of the smaller block when it reaches the top of the bigger block.

My concern is while using energy conservation to the system of the two blocks,
can we get the same equation using work energy theorem (WET) to individual blocks and finally adding them.

While using WET to the individual blocks,I am unable to write the equations for the works of the normal reactions between the blocks in the curved parts as the normal reaction vanishes on the vertical portion and not getting how the works will be canceled to give the required equation.

 

[jbriggs444]

and not getting how the works will be canceled to give the required equation.

I do not have much advice to offer on how to compute the individual works. But the fact that their sum is zero is fairly easy to derive.

We care about the dot product of the contact force from ramp on puck and the velocity of the puck. This is the instaneous mechanical power delivered to the puck.

We care about the dot product of the contact force from puck on ramp and the velocity of the ramp. This is the instantaneous mechanical power delivered to the ramp.

We want to demonstrate that the two dot products are equal and opposite at all times. Therefore their integrals will be equal and opposite, therefore the cumulative works done by each on each other are equal and opposite.

The contact force between the two blocks has a normal component and a tangential component. We are told that friction is zero. So the tangential component is zero.

The velocities of each of the two blocks have a normal component and a tangential component. The tangential components will not contribute to either dot product. So we can ignore them. We are left with the two normal components.

The two normal forces are equal and opposite. Because Newton's third.
The two normal velocities are equal. Because the two surfaces remain in contact.

Therefore the two dot products are equal and opposite at all times.

Is that the sort of thing that you were after?

 

[sachin]

sorry,did not get the normal and tangential components of contact forces and velocities,will request if u can add a picture on the same,thanks.

 

[kuruman]

Is that the sort of thing that you were after?

I cannot speak for the OP, but I think that OP wants to consider each block separately as a system, use the WE theorem to find the kinetic energy change of each block and the net work done by gravity and the other block and then show that the sum of kinetic energy changes is equal to the sum of the external works. I think it can be done if one assumes a shape for the track, probably a circle would be the easiest. The shape is necessary to calculate the work done by the horizontal component of the normal force as a function of angle.

 

[sachin]

Is my assumption correct,that adding work energy theorems to individual blocks an finally adding them,we get the equation of energy consrvation of the system of blocks.

 

[sachin]

the curve part is part of a circle.

 

[Steve4Physics]

Some thoughts:

1/2 mv2 = 1/2 mvx2 + 1/2 mvy2 + 1/2 Mvx2

Your energy-balance equation ignores the gravitational potential energy gained by the small block (i.e you have ignored the work done by gravity).

In addition:

The question could be asking about the case where the small block only just reaches the top of the big block. This would simplify the problem. You might want to check.
Edit: above paragra[h deleted - not necessary.

Don't forget conservation of momentum.

 

[sachin]

Some thoughts:Your energy-balance equation ignores the gravitational potential energy gained by the small block (i.e you have ignored the work done by gravity).

In addition:

The question could be asking about the case where the small block only just reaches the top of the big block. This would simplify the problem. You might want to check.

Don't forget conservation of momentum.

Some thoughts:Your energy-balance equation ignores the gravitational potential energy gained by the small block (i.e you have ignored the work done by gravity).

In addition:

The question could be asking about the case where the small block only just reaches the top of the big block. This would simplify the problem. You might want to check.

Don't forget conservation of momentum.

I have taken gravity into consideration while framing the system equation,my concern was how the works of normal forces not coming in it,thanks.

 

[Steve4Physics]

I have taken gravity into consideration while framing the system equation,my concern was how the works of normal forces not coming in it,thanks.

You have: 1/2 mv2 = 1/2 mvx2 + 1/2 mvy2 + 1/2 Mvx2

Your equation says:
(initial kinetic energy) = (final kinetic energy of small block) + (final kinetic energy of large block)

But this can’t be true - because the small block has gained gravitational potential energy ($mgh$). Where has this gravitational potential energy come from?

There is no need to use normal forces. They make the solution harder in my opinion. However, if you want to use them, remember that the vertical component of the normal force on the small block does some work: this work is the increase in gravitational potential energy.

Also, did you check that you correctly understaood the question as suggested in Post #7?
Edit: above sentence deleted. The question is Ok as it is.

Note that using Latex, your (incorrect) equation will look like much neater like this:
$\frac 1 2 mv^2 = \frac 1 2 mv_x^2 + \frac 1 2 mv_y^2 + \frac 1 2 Mv_x^2$
(See link to Latex Guide at bottom left of message-area when writing a message.)

 

[haruspex]

It is not possible to solve it using work alone. You must either appeal to momentum conservation or consider forces as a function of time. But of course, those are the same thing. I.e. if you were to write all the forces and motions as functions of time you should in principle be able to obtain the horizontal momentum conservation equation without needing to specify the curve.