Approach to extrapolate a "superpositioned" wave?

[ironhak]

TL;DR Summary

Trying to find an approach to extrapolate a super-imposed wave (noob in physics)

Hello everyone, sorry if this is the wrong section. In this forum I'm a fish out of the bowl, my knowledge of physics is ages beyond most of the people on there, so please forgive my naivness.

So, here's my problem, I'm a sort of "audio" engineer (won't enter much on detail) and on my free time I like to entertain myself with quantum physics content. A couple of days ago I had a problem to solve, let's say I have a wave like this:

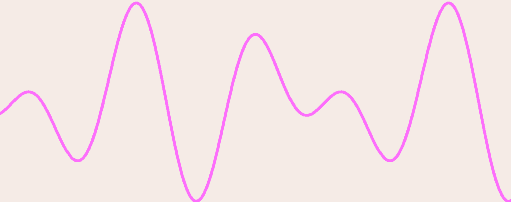
Actually, what I'm dealing with is far more complex, but that's just an example. Basically I need to study in depth that wave and find out the reason for every turning point, basically I need to see all the waves contained on that resultant wave, like this:

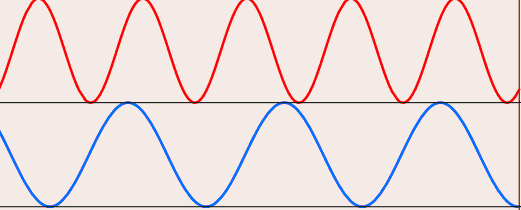
In fact red and blue wave create purple wave. On my real life case I have the purple wave and from it I need to find blue and red waves (and potentially many more). Now, of course I don't need a perfect match result, just a rough estimation is good.

From a logical point of view (no formulas please), how would you proceed? Brute forcing a lot of different simple waves until a suited combination comes out is an idea that I got, but that's not doable, the solution must be more simple and intuitive. Ideas?

Mods, please if this is the wrong section move the thread to the right one. Thank's everyone!

 

[Dale]

TL;DR Summary: Trying to find an approach to extrapolate a super-imposed wave (noob in physics)

From a logical point of view (no formulas please), how would you proceed?

This is the purpose of the Fourier transform. It is math, so there is no avoiding that if you want to go any deeper, but it is already implemented in a lot of different software packages.

 

[ironhak]

This is the purpose of the Fourier transform. It is math, so there is no avoiding that if you want to go any deeper, but it is already implemented in a lot of different software packages.

Hello, thanks for stopping by!

Can I ask you what are the principles beyond Fourier transform? I mean, from a logical standpoint, how does it proceed to extrapolate different waves from a main one?

 

[Dale]

(no formulas please)

Can I ask you what are the principles beyond Fourier transform? I mean, from a logical standpoint, how does it proceed to extrapolate different waves from a main one?

You are going to have to make a choice. I cannot talk about details without math. All I can say without math is that it takes an input signal and splits it into all of the different frequencies that make the input signal.

Without math it is a black box, and if you open the black box you will find math.

 

[Ibix]

Hello, thanks for stopping by!

Can I ask you what are the principles beyond Fourier transform? I mean, from a logical standpoint, how does it proceed to extrapolate different waves from a main one?

It turns out that if you multiply two sine waves together and work out the total area between the result and the axis (area below the axis counts as negative) the answer is zero - except if the two waves have the same frequency. So multiplying an arbitrary wave by a sine wave at frequency $f$ and computing the area under the curve gives you the amount of frequency $f$ sine wave contributing to the arbitrary wave. The Fourier transform provides a neat mathematical way of doing that for all frequencies in one pass, so you don't have to do infinite multiplications and area calculations. Applying it to your example would give you a flat line at zero with two spikes, one at each of the frequencies of your input waves.

The result is usually a complex number, the argument of which tells you about how the waves are shifted from crossing the axis at the same place. I don't think there's a way to say that without maths.

 

[Baluncore]

Basically I need to study in depth that wave and find out the reason for every turning point, basically I need to see all the waves contained on that resultant wave, like this: ...

Spectrum analysis is the conversion of a wave in the time domain, into its sinewave components, each with a frequency and phase.

The Fourier transform generates the frequency spectrum from the time domain. The inverse Fourier transform generates the time domain signal from the frequency spectrum.

If turning points are of critical interest, then you are going to have more problems than most audio engineers, since the phase of the harmonics will then be critical. In general, the cochlea of your ear, does not analyse the phase of the harmonics of a signal.

To extrapolate a waveform, you must have a repeating waveform, or you must analyse the phase of the individual sinewave components, then extrapolate those and form the sum.

 

[ironhak]

You are going to have to make a choice. I cannot talk about details without math. All I can say without math is that it takes an input signal and splits it into all of the different frequencies that make the input signal.

Without math it is a black box, and if you open the black box you will find math.

Ok, perhaps could you try to explain just the basic formula behind it?

 

[ironhak]

It turns out that if you multiply two sine waves together and work out the total area between the result and the axis (area below the axis counts as negative) the answer is zero - except if the two waves have the same frequency. So multiplying an arbitrary wave by a sine wave at frequency $f$ and computing the area under the curve gives you the amount of frequency $f$ sine wave contributing to the arbitrary wave. The Fourier transform provides a neat mathematical way of doing that for all frequencies in one pass, so you don't have to do infinite multiplications and area calculations. Applying it to your example would give you a flat line at zero with two spikes, one at each of the frequencies of your input waves.

The result is usually a complex number, the argument of which tells you about how the waves are shifted from crossing the axis at the same place. I don't think there's a way to say that without maths.

Thank you, could you please explain me better this part:

if you multiply two sine waves together and work out the total area between the result and the axis (area below the axis counts as negative) the answer is zero

 

[Dale]

Ok, perhaps could you try to explain just the basic formula behind it?

Sure, the basic formula is: $$F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i 2\pi \omega t} dt$$ This takes a signal $f(t)$ and compares it to each possible frequency $e^{-i 2 \pi \omega t}$ to get the amount of the signal $F(\omega)$ that is contributed by each frequency $\omega$.

You can then get the "red" or "blue" waves as follows: for any frequency $\omega$ the wave is $$\mathrm{Re}[F(\omega)] \cos(\omega t) + \mathrm{Im}[F(\omega)]\sin(\omega t)$$

 

[hutchphd]

Thank you, could you please explain me better this part:

These need to be waves of different frequencies. Then their product will average (over long times) to exactly zero because it will be positive and then negative equally regardless of initial relative phase.

 

[Ibix]

Thank you, could you please explain me better this part:

I'm not sure what you don't understand. You obviously know how to add functions, and multiplying them should therefore straightforward. And the area between a curve and the x axis doesn't seem an especially complex concept. What didn't you follow?

 

[ironhak]

I'm not sure what you don't understand. You obviously know how to add functions, and multiplying them should therefore straightforward. And the area between a curve and the x axis doesn't seem an especially complex concept. What didn't you follow?

So you're saying that:

$f(x)\cdot f(z) = 0$

??

Sorry maybe I didn't understood, but isn't the purple wave wrong? It should be the superposition of red and blue.

 

[hutchphd]

Given two sin functions $A\sin k_1 x$, $B\sin k_2 x$, plot them and their product for some values. Notice only if k1=k2 is the product average nonzero

 

[ironhak]

Given two sin functions $A\sin k_1 x$, $B\sin k_2 x$, plot them and their product for some values. Notice only if k1=k2 is the product average nonzero

Sorry, maybe I don't get it. There are two equal waves, but they don't cancel each other

 

[Baluncore]

Notice only if k1=k2 is the product average nonzero

If the system is linear, then the waves will be simply added, they will NOT be multiplied.

Don't forget that the A = V * Cos( 0 ) component is a DC offset from zero.

 

[hutchphd]

If the system is linear, then the waves will be simply added, they will NOT be multiplied.

I was attempting (apparently badly as it turns out ) to explain the formal process of finding the various Fourrier coefficients. You multiply the target function by the sin function and the integral pulls out the frequency you want.......the OP said no math.
No Royal Road, I guess

 

[ironhak]

Sorry guys this is not my field, I was just trying to get some inspiration to solve my problem. Thank's for your kindly explainations, clearly I do not understand because I do not have any solid physics/math background, not because you lack of explaination skills. I'll try to read in repetition your answers until maybe I'll understand.

Thank's everyone

 

[Baluncore]

A good introduction without mathematics.
https://en.wikipedia.org/wiki/Fourier_analysis

 

[ironhak]

Thank's

 

[Ibix]

So you're saying that:
View attachment 321866
$f(x)\cdot f(z) = 0$

No. The product of two functions (by the way, they need to be different functions of the same thing, so $f(x)$ and $g(x)$ for example, not $f(x)$ and $f(z)$, which is the same function of different things) is generally not zero. However, remember that we're talking about sine waves in particular. Their product is still not zero. But the total area between the curve and the x axis can be zero anyway - remember that if the line is above the axis the area is positive and if it's below the axis it's negative. Sine is a very repetitive function which is positive just as much as it is negative, and therefore the total area between it and the axis is zero because every positive bit has a negative bit to match.

That extends to the product of two sine functions, the area under which is also zero - except when the sine waves are exactly the same frequency. In that case the two sine functions are positive at the same place (so their product is positive) and negative at the same place (so their product is also positive) so the area under the product is not zero. That lets you "pick out" how much of a particular frequency sine wave there is in a function by multiplying by the sine you are interested in and summing the area of the result.

 

[snorkack]

That extends to the product of two sine functions, the area under which is also zero - except when the sine waves are exactly the same frequency. In that case the two sine functions are positive at the same place (so their product is positive) and negative at the same place (so their product is also positive) so the area under the product is not zero. That lets you "pick out" how much of a particular frequency sine wave there is in a function by multiplying by the sine you are interested in and summing the area of the result.

Does not actually follow.
If you combine two sine functions of different frequency, it is true that they are going to beat.
If what you are doing to the two sines is summing, the result of beating will depend on the relative amplitude of the two sines - whether they are same amplitude or different. But if what you are doing is multiplying them then the product will be zero wherever either of them is zero regardless of amplitude.
If the sines are different amplitude then in some parts they will be same phase (and have positive product), and in some parts they will be opposite phase (and have negative product). Over the beats, the sum of the positive and negative product parts will be zero. This far is true.

If you multiply two sines of exact same frequency but opposite phase (differing by 180 degrees) then there will be no beating but the product will never be positive - it will always be negative.

And if you multiply two sines of exact same frequency but at quadrature (differing by 90 degrees) then there will be no beating but the product will also sum up to 0, just the same as if the frequencies were different. Think of it. From 0° to 90°, sin x goes from 0 to 1 but sin (x+90°) goes from 1 to 0, so positive product. From 90° to 180°, sin x goes from 1 to 0, but sin (x+90°) goes from 0 to -1 so negative product. From 180° to 270°, sin x goes from 0 to -1 but sin (x+90°) goes from -1 to 0, so positive product. From 270° to 0°, sin x goes from -1 to 0 but sin (x+90°) from 0 to 1 so negative product. The quarters will cancel out pairwise.

Presumably there are mathematical ways to resolve it, so checking for wavelength distribution is less vulnerable to choice of phase of test wave? As stated before, Fourier transformed frequency spectrum won´t give you the original waveform because frequency spectrum omits information about the relative phases of the components.

 

[hutchphd]

Does not actually follow.

This is true but irrelevant. The OP wanted no math.

 

[Ibix]

Presumably there are mathematical ways to resolve it,

Yes - the Fourier transform actually uses a complex exponential rather than just a sine (see #9), which deals with the phase issue. Not mentioning it was a judgement call about how far "no maths" can take the OP.

 

[Swamp Thing]

... I need to see all the waves contained on that resultant wave ...

From a logical point of view (no formulas please), how would you proceed?

This is a very good starting point:



And this:



After which the math based learning curve would likely appear less off-putting. To some extent, you may be able to use ready-made tools to do what you want, without deep-diving into how they work. For example, there are mobile phone apps that will take the sound from the microphone and display the frequency breakdown on a graph called a spectrum, and you can easily learn to interpret the spectrum in terms of a bunch of sine waves.

 

[vanhees71]

Sure, the basic formula is: $$F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-i 2\pi \omega t} dt$$ This takes a signal $f(t)$ and compares it to each possible frequency $e^{-i 2 \pi \omega t}$ to get the amount of the signal $F(\omega)$ that is contributed by each frequency $\omega$.

You can then get the "red" or "blue" waves as follows: for any frequency $\omega$ the wave is $$\mathrm{Re}[F(\omega)] \cos(\omega t) + \mathrm{Im}[F(\omega)]\sin(\omega t)$$

I'd rather write
$$F(\omega)=\int_{-\infty}^{\infty} \mathrm{d} t f(t) \exp(-\mathrm{i} \omega t),$$
or if you want to have not the angular frequencies but usual freqencies, $f=\omega/(2 \pi)$
$$\tilde{F}(f)=\int_{-\infty}^{\infty} \mathrm{d} t f(t) \exp(-\mathrm{i} 2 \pi f t).$$
Concerning the sign in the exponential that's the "engineering convention" of the Fourier transformation.

It can drive you nuts if you are used to the physicist's convention ;-)).

 

[snorkack]

Yes - the Fourier transform actually uses a complex exponential rather than just a sine (see #9), which deals with the phase issue. Not mentioning it was a judgement call about how far "no maths" can take the OP.

But then have a look at explaining the thing with minimal mathematics. Next posts use integral sign naturally.
Remember that integral is a somewhat complicated development of sum (infinite sum), so start by explaining the properties of integral through the properties of sums and the function inside the integral.

Now when you "combine" two sine waves, how can you do it?
You can add the sines. Then the addition formula goes
sin a + sin b = 2 * sin ((a+b)/2) * cos ((a-b)/2)
Note that since one of the factors is sin ((a+b)/2), the combined wave will still go through zero each period. It will be oscillating around zero. The slow beat from combining two waves of close but different frequencies will be in form of amplitude modulation with the constant zero point. When you manage exact frequency match, b=a+x, the slow beat slows down and stops, to
sin a+sin(a+x)=2*sin (a+x/2)*cos(-x/2).
This beat goes through zero value always but zero amplitude only if the component amplitudes match. If what you have is like sin a+2*sin b, it will have a beat but not to zero amplitude.
Or you can multiply the sines. The multiplication formula is
sin a*sin b=(cos(a-b)-cos(a+b))/2.
Note that when a is close to b, you have immediately doubled the frequency, which did not happen when you added the sines: sin² a=sin a*sin a=(cos 0-cos 2a)/2=(1-cos 2a)/2!
Also note that you added a direct current component: your slow beat will not be amplitude modulation but low frequency oscillation of the average, and as the beat slows down to stop, it turns in a direct current.
I pointed out that with an unlucky choice of test wave, you might miss out the direct current:
sin a*sin(a+90°)=((cos -90°)-cos (2a+90°))/2, and cos -90°=0. But this is handled by using complex wave. Since the Euler formula is:
e^ix=cos x+i sin x
what multiplication with complex wave does is that the wave being tested is simultaneously subjected to test multiplication with two waves at 90 degrees from each other (but same frequency) and the results tracked separately. Comparing the two will give the phase of the wave being tested compared to the test wave.

So, if you try to figure out what the Fourier transform does:
You take your sample wave which is a sum of unknown waves, but with no DC component.
Then you multiply it with your test wave, or strictly speaking a pair of test waves of the same frequency and 90 degree phase from each other.
The components of your sample wave which are far from test wave frequency will produce high frequency oscillations. The components which are close to the test wave frequency but not exactly right will produce slow beat oscillation but over the long time of integration, it is still oscillation that integrates to zero. The components of sample that make an exact match to the test wave will produce a DC current - or at least one of the pair of the test waves will.
And then you scan through the frequency range to identify frequencies where some component of your sample will give the beat that slows down to DC.

 

[sophiecentaur]

TL;DR Summary: Trying to find an approach to extrapolate a super-imposed wave (noob in physics)

In fact red and blue wave create purple wave.

I wouldn't recommend going down this route. 'Purple' is a colour and colours are only in your head. your eye sees the two waves (and they are always distinct and separate entities) and you are aware of their relative amplitudes. Your brain interprets this ratio as a 'colour'. That's all.

In nearly every discussion about light, it is the wavelengths and the amplitudes that count. You can analyse light with a spectrometer and that will tell you the relative amplitudes of the different wavelengths. Your eye is not a spectrometer. It's very clever but we didn't evolve a need for spectral analysis and so we did the next best thing and we 'see' colour'.

To nail this down, further; you can look at a combination of red and green light (the spectrum) and your eye will 'see' yellow but there are no yellow wavelengths in the mixture. OTOH, you can burn Sodium metal and the yellow light that emerges is a wave with just one spectral wavelength (looks Yellow.)

In the case of your 'Purple', there is no single wavelength of light that appears as Purple - it is a non-spectral colour.

 

[sophiecentaur]

TL;DR Summary: Trying to find an approach to extrapolate a super-imposed wave (noob in physics)

From a logical point of view (no formulas please), how would you proceed?

This is the purpose of the Fourier transform. It is math, so there is no avoiding that

If you had a drawer full of (thousands of) optical filters that only pass a very narrow range of wavelengths of light then only two filters would let anything through; a particular red and a particular blue wavelength. There's no actual Maths in that but, of course, the guy who designed the filters would have used Maths. That Maths would have involved some form of 'transform' because very selective optical filters are very hard and very expensive.