Approximate the probability of tunneling

[AntiStrange]

Homework Statement

Consider the harmonic scillator potential perturbed by a small cubic term, so that
V(x) = \frac{1}{2}m\omega^{2} (x^{2} - \frac{x^{3}}{a})
if a is large compared to the characteristic dimension (\hbar /m\omega)^{1/2}, the states will all me metastable, since there can be no lowest energy state (as x\rightarrow\infty, the energy gets arbitrarily negative). Estimate the probability of tunneling from the ground state to the region on the far right.

Homework Equations

probability = |T|^{2} = e^{-2\int^{a}_{0} dx \sqrt{2m(V-E)/\hbar^{2}}}

The Attempt at a Solution

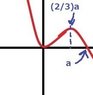
A rough sketch of what the potential should look like when graphed is attached. However, I cut out the \frac{1}{2}m\omega^{2} part at the front (is that bad?) but anyway that is what x^{2}-x^{3}/a looks like. it crosses the x-axis at x=0 and x=a, and the maximum on the right side is at (2/3)a.

I have tried several things. Just substituting the potential given in the problem and I'm using E = (1/2)*h-bar*omega as the energy (ground state of the harmonic oscillator), into the equation but I can't solve the integral, even an online automatic integrator doesn't figure it out.
I have also tried equating the potential to the energy using the E = (1/2)*h-bar*omega and setting that equal to the potential and solving for omega. even though I'm not sure I am allowed to do this, it simplifies things a little bit, but the integral still seems impossible to solve.
I have also tried to approximate the curve on the right side by a negative parabola, perhaps it would work but I am having some trouble finding a parabola that fits close enough.

Any help would be very appreciated, or a point in the right direction.

 

[gabbagabbahey]

Homework Equations

probability = |T|^{2} = e^{-2\int^{a}_{0} dx \sqrt{2m(V-E)/\hbar^{2}}}

That doesn't look right...Shouldn't the probability that a particle tunnels over the barrier into the far right be given by

T=\int_{\frac{2a}{3}}^{\infty} |\psi(x)|^2 dx

?