- #1
WMDhamnekar
MHB
- 381
- 28
Write a program that uses the Monte Carlo method to approximate the double integral $\displaystyle\iint\limits_R e^{xy}dA$ where $R = [-1,1] \times [0, x^2]$. Show the program output for N = 10, 100, 1000, 10000, 100000 and 1000000 random points.
My correct answer:
My Java program:
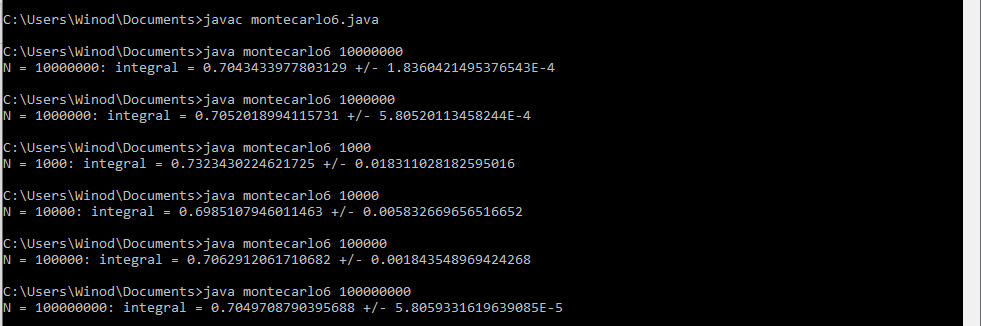
The above program's output:
My correct answer:
My Java program:
Java:
//Program to approximate the double integral of f(x,y)=e^xy over the
//region bounded by x=-1, x=1, y=0, and y=x^2
public class montecarlo6 {
public static void main(String[] args) {
//Get the number N of random points as a command-line parameter
int N = Integer.parseInt(args[0]);
double x = 0; //x-coordinate of a random point
double y = 0; //y-coordinate of a random point
double f = 0.0; //Value of f at a random point
double mf = 0.0; //Mean of the values of f
double mf2 = 0.0; //Mean of the values of f^2
for (int i=0;i<N;i++) { //Get the random coordinates
x = 1 * Math.random() ; //x is between 1 and 0
y = 1 * Math.random() ; //y is between 0 and 1
if (y < Math.pow(x,2)) { //the point is in the region
f = Math.exp(x*y); // Value of the function
mf = mf + f; //Add to the sum of the f values
mf2 = mf2 + f*f; //Add to the sum of the f^2 values
}
x = -1 * Math.random() ; //x is between -1 and 0
y = Math.random() ; //y is between 0 and 1
if (y < Math.pow(x,2)) { //the point is in the region
f = Math.exp(x*y); // Value of the function
mf = mf + f; //Add to the sum of the f values
mf2 = mf2 + f*f; //Add to the sum of the f^2 values
}
}
mf = mf/N; //Compute the mean of the f values
mf2 = mf2/N; //Compute the mean of the f^2 values
System.out.println("N = " + N + ": integral = " + vol()*mf +
" +/- " + vol()*Math.sqrt((mf2 - Math.pow(mf,2))/N));
}
//The volume of the rectangle [-1,1]x[0,1]
public static double vol() {
return 1*1;
}
}The above program's output:
Attachments
Last edited:
