plum356
- 10
- 5
Good evening!
Have a look at the following part of a proof:
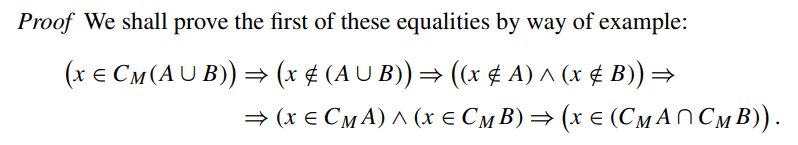
Mentor note: Fixed the LaTeX
I don't understand the use of implications. Isn't ##x\in C_M(A\cup B)\iff x\notin(A\cup B)##? To me, all of these predicates are equivalent.
Have a look at the following part of a proof:
Mentor note: Fixed the LaTeX
I don't understand the use of implications. Isn't ##x\in C_M(A\cup B)\iff x\notin(A\cup B)##? To me, all of these predicates are equivalent.
Last edited by a moderator:
