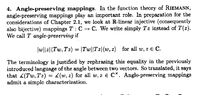Are Injective R-Linear Mappings in C Necessarily Surjective?

[Math Amateur]

I am reading Reinhold Remmert's book "Theory of Complex Functions" ...

I am focused on Chapter 0: Complex Numbers and Continuous Functions ... and in particular on Section 1.4: Angle-Preserving Mappings ... ...

I need help in order to fully understand a remark of Remmert's regarding injective $$\mathbb{R}$$-linear mappings The relevant part of Remmert's section on Angle-Preserving Mappings reads as follows:View attachment 8550In the above text from Remmert we read the following:

" ... ... we look at $$\mathbb{R}$$-linear injective (consequently also bijective) mappings $$T : \mathbb{C}\to \mathbb{C}$$ ... ... " Can someone please explain how/why exactly $$\mathbb{R}$$-linear injective mappings are necessarily surjective ... ... ?

Peter

 

[Opalg]

In the above text from Remmert we read the following:

" ... ... we look at $$\mathbb{R}$$-linear injective (consequently also bijective) mappings $$T : \mathbb{C}\to \mathbb{C}$$ ... ... "

Can someone please explain how/why exactly $$\mathbb{R}$$-linear injective mappings are necessarily surjective ... ... ?

Considered as a vector space over $\Bbb{R}$, $\Bbb{C}$ is a two-dimensional space. It is a theorem from linear algebra (the rank-nullity theorem) that the rank plus the nullity of a linear map on a vector space equals the dimension of the space. In this case, if the mapping is injective then its nullity is zero, so its rank is equal to the dimension of the space. That is equivalent to saying that the map is surjective, and therefore bijective.