Trying2Learn
- 375
- 57
- TL;DR Summary
- From the schematic to the real.
Goooood Morning all!
I am going through a few problems in advanced dynamics with Hamilton's Principle.
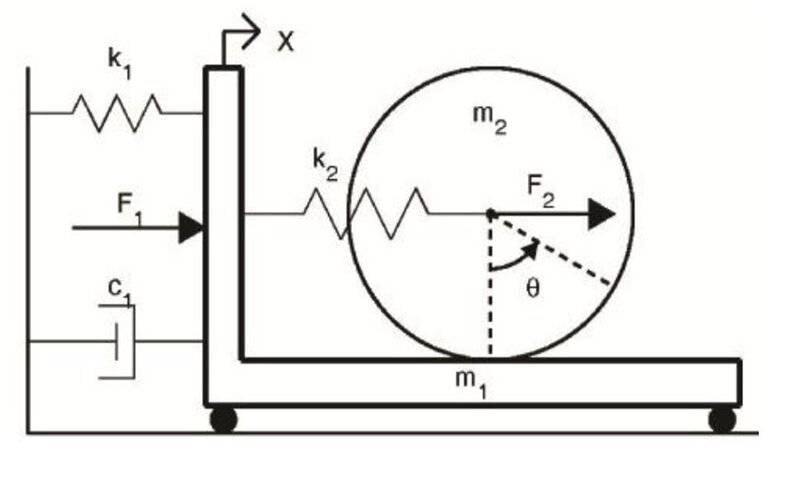
One of them is shown above (this is NOT a question about the solution)
The spring constants, damping, mass, force, are all given. So, too, is the constraint: large disk rolls without slipping.
My question is this: Does such a mechanical device exist?
I suppose one could replace the "rolling without slipping" constraint with "rack and pinion" gear set.
I am going through a few problems in advanced dynamics with Hamilton's Principle.
One of them is shown above (this is NOT a question about the solution)
The spring constants, damping, mass, force, are all given. So, too, is the constraint: large disk rolls without slipping.
My question is this: Does such a mechanical device exist?
I suppose one could replace the "rolling without slipping" constraint with "rack and pinion" gear set.
- But is this specific schematic representative of some real device?
- And, more generally, but just as important to me: as I go through such examples, how can I find out if the schematics for the varied problems exists?
- Or should I content myself with realizing that these are indeed simple schematics to learn the language of how to apply Hamilton's Principle? (much like found in electrical circuitry examples)