Area congruence in two quadrilaterals

  • MHB
  • Thread starter My Name is Earl
  • Start date
  • Tags
    Area
In summary: I contacted the author of the book. To my surprise I got a quick response. He stated that the problem is not solvable without saying that EFGA is a parallelogram. There was an error during the printing process and the problem was supposed to state this fact. Problem solved!
  • #1
My Name is Earl
12
0
Using the theorems:
Area of a triangle = (1/2)bh
Area of a parallelogram = bh
Area of a trapezoid = (1/2)h(b1+b2)
Solve the following:

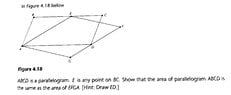
View attachment 8517
 

Attachments

  • parallelogram.jpg
    parallelogram.jpg
    67.7 KB · Views: 97
Mathematics news on Phys.org
  • #2
Hint ...

triangle AED contains half the area of both given parallelograms
 
  • #3
skeeter said:
Hint ...

triangle AED contains half the area of both given parallelograms

That is true if you assume quadrilateral EFGA is a parallelogram. Only quadrilateral ABCD is defined as a parallelogram. You would have to prove that EFGA is a parallelogram, then the problem becomes easy using area formulas. How do you prove that EFGA is a parallelogram with the given information?
 
  • #4
My Name is Earl said:
That is true if you assume quadrilateral EFGA is a parallelogram. Only quadrilateral ABCD is defined as a parallelogram. You would have to prove that EFGA is a parallelogram, then the problem becomes easy using area formulas. How do you prove that EFGA is a parallelogram with the given information?

We can't prove that EFGA is a parallelogram.
It could be any type of quadrilateral, and we can't say anything about its area either.
Note that we can pick F anywhere we want, and after picking F we can pick G anywhere on the line DF.

In other words, it seems that the problem statement should have said that EFGA is a parallelogram, and that it was accidentally left out.
 
  • #5
I find it strange that there is no reference to the position of point $D$.
 
  • #6
Klaas van Aarsen said:
We can't prove that EFGA is a parallelogram.
It could be any type of quadrilateral, and we can't say anything about its area either.
Note that we can pick F anywhere we want, and after picking F we can pick G anywhere on the line DF.

In other words, it seems that the problem statement should have said that EFGA is a parallelogram, and that it was accidentally left out.

I spent days on this one to no avail. I can pick an E such that AE is parallel to GF, but that does not allow me to show that AE = GF. I really believe the author meant EFGA not to be initially defined as a parallelogram. I sure do wish I could see their solution to this one. Thanks for the reply!
 
  • #7
My Name is Earl said:
I spent days on this one to no avail. I can pick an E such that AE is parallel to GF, but that does not allow me to show that AE = GF. I really believe the author meant EFGA not to be initially defined as a parallelogram. I sure do wish I could see their solution to this one. Thanks for the reply!

I contacted the author of the book. To my surprise I got a quick response. He stated that the problem is not solvable without saying that EFGA is a parallelogram. There was an error during the printing process and the problem was supposed to state this fact. Problem solved!
 

FAQ: Area congruence in two quadrilaterals

What is area congruence in two quadrilaterals?

Area congruence in two quadrilaterals refers to the property of two quadrilaterals having the same area. This means that the two shapes have the same amount of space inside them, even if their side lengths and angles may be different.

How is the area of a quadrilateral calculated?

The area of a quadrilateral can be calculated using the formula A = (1/2)*b*h, where b is the length of the base and h is the height of the quadrilateral. Alternatively, if the quadrilateral is divided into triangles, the area can be calculated using the formula A = (1/2)*b1*h1 + (1/2)*b2*h2, where b1 and b2 are the lengths of the bases of the two triangles and h1 and h2 are the heights of the two triangles.

How do you prove area congruence in two quadrilaterals?

To prove that two quadrilaterals are congruent in area, you must first show that all corresponding pairs of sides are congruent, and then show that the corresponding pairs of angles are also congruent. This can be done using geometric theorems and properties, such as the Side-Side-Side (SSS) and Angle-Angle-Side (AAS) congruence criteria.

Why is area congruence important in geometry?

Area congruence is important in geometry because it allows us to compare the sizes of different shapes. By knowing that two shapes have the same area, we can make statements about their relative sizes and properties. Area congruence is also used in real-world applications, such as determining the amount of material needed for construction projects.

What are some real-life examples of area congruence in two quadrilaterals?

One example of area congruence in two quadrilaterals is when two different shaped plots of land have the same amount of area. This means that they can be used for the same purpose, such as building a house, even though their shapes may be different. Another example is in quilting, where different shaped pieces of fabric can be cut and sewn together to create a quilt with the same overall area.

Similar threads

MHB Prove Quadrilateral Divider: Equal Area & Perimeter
Replies
4
Views
2K
MHB Maximum area of rectangle which circumscribes the given quadrilateral.
Replies
21
Views
3K
MHB What is the area of the quadrilateral?
Replies
1
Views
1K
MHB [ASK] Find the ratio of the area of triangle BCH and triangle EHD
Replies
4
Views
1K
B Probability - two possible points of view?
Replies
7
Views
1K
MHB How Do You Calculate the Area of a Shaded Segment of a Circle?
Replies
1
Views
1K
MHB Max Area of Simple Quadrilateral w/ Sides $a$ & $b$: Justification
Replies
4
Views
2K
MHB Area of Triangle ABC Given Dimensions
Replies
5
Views
2K
Formulae for calculating the area of a quadrilateral non-cyclic
Replies
2
Views
2K
MHB Find the areas of segment in circle
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top