- #1
magnetpedro
- 39
- 0
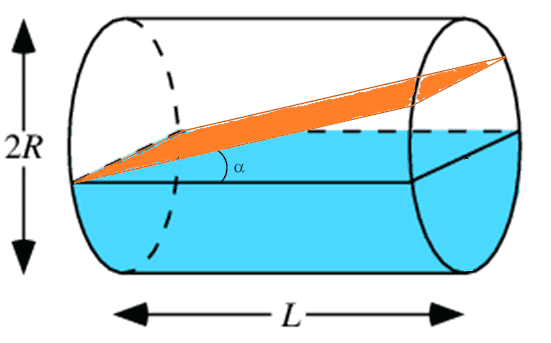
What is the equation of the area of the trapezoid when a cylinder of radius R is cut by a plane inclined at an angle α? (Orange area of the figure)
How can I relate it with Abase=π*R2 or with Ainside=2*R*L?
Any hints please?
Thank you very much in advance.
How can I relate it with Abase=π*R2 or with Ainside=2*R*L?
Any hints please?
Thank you very much in advance.