Area Problem - Find the Answer | Susanto

[susanto3311]

hi all...

View attachment 4099

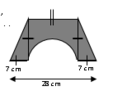
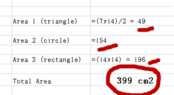
please, see my picture, the area is...

a) 217 cm2
b) 434 cm2
c) 154 cm2
d) 294 cm2

thanks in advance...

susanto

 

[I like Serena]

hi all...

please, see my picture, the area is...

a) 217 cm2
b) 434 cm2
c) 154 cm2
d) 294 cm2

thanks in advance...

susanto

Hey susanto3311! ;)

What would be the radius of the circle?

 

[susanto3311]

Hey susanto3311! ;)

What would be the radius of the circle?

the radius is 28 - (2x7) = 14 cm..

it's true?

 

[I like Serena]

the radius is 28 - (2x7) = 14 cm..

it's true?

Almost. That's the diameter. The radius is half of that.

What would be the height? (Wondering)

 

[susanto3311]

Almost. That's the diameter. The radius is half of that.

What would be the height? (Wondering)

hi Serena, i don't know?could you show me...

 

[I like Serena]

hi Serena, i don't know?could you show me...

The cross stripes seem to indicate a height of 2x7=14 cm.

Now which parts does the area consist of and what are their areas?
I think you should be able to find those by now...

 

[susanto3311]

The cross stripes seem to indicate a height of 2x7=14 cm.

Now which parts does the area consist of and what are their areas?
I think you should be able to find those by now...

i still confuse...how do make more easy?

 

[I like Serena]

i still confuse...how do make more easy?

Please, could you give some indication of where you are stuck?
Or what you are thinking?

 

[susanto3311]

Please, could you give some indication of where you are stuck?
Or what you are thinking?

hello Serena,

here my problem..
View attachment 4100

 

[I like Serena]

hello Serena,

here my problem..

Good! (Smile)

You have already found that the diameter at the bottom is 14 cm.
So the distance at the top should also be 14 cm.

As for the diagonals of the triangles, you don't need them.
But if you want, you can calculate them using the Pythagorean Theorem $a^2+b^2=c^2$. Or more to the point: $c = \sqrt{a^2+b^2}$.

On the left you have a right triangle with base 7 and height 14.
Do you know how to calculate its area? (Wondering)

 

[susanto3311]

Good! (Smile)

You have already found that the diameter at the bottom is 14 cm.
So the distance at the top should also be 14 cm.

As for the diagonals of the triangles, you don't need them.
But if you want, you can calculate them using the Pythagorean Theorem $a^2+b^2=c^2$. Or more to the point: $c = \sqrt{a^2+b^2}$.

On the left you have a right triangle with base 7 and height 14.
Do you know how to calculate its area? (Wondering)

hi Serena,

i think like this..

it's all true answer?

 

[I like Serena]

hi Serena,

i think like this..

it's all true answer?

You have the right parts with the right areas. Good!

However, they should not simply be summed.
- You should have 2 triangles of 7x14 instead of 1.
- There is only half of a circle, so its area should be divided by 2.
- The half circle is something that has been removed from the object. So instead of adding it, it should be subtracted.
(Thinking)

 

[MarkFL]

Another way to approach this would be to find the area $A_T$ of the trapezoid (all areas in $\text{cm}^2$):

$$A_T=\frac{h}{2}(B+b)$$

Now find the area $A_S$ of the semi-circle:

$$A_S=\frac{\pi}{8}d^2$$

And so the area $A$ of the given figure is:

$$A=A_T-A_S=\frac{h}{2}(B+b)-\frac{\pi}{8}d^2$$

You know all of the following:

$h$ = height of trapezoid

$B$ = "big" base of trapezoid

$b$ = "little" base of trapezoid

$d$ = diameter of semi-circle

So now just plug the numbers in, and round to the nearest integer. What do you find?

 

[susanto3311]

maybe, i have try..

 

[I like Serena]

maybe, i have try..

Yep! That's it! (Happy)

One improvement: for area 1 you should have {(7x14)/2}x2 = 49x2 = 98, but that's what you used anyway.

 

[susanto3311]

hi..

why different result with 2 method :

like this ..

where is something wrong?

 

[I like Serena]

hi..

why different result with 2 method :

like this ..

where is something wrong?

The symbols are mixed up.
The diameter d should be 14 cm.
The "big" base B should be 28 cm.
And the "little" base b should be 14 cm.