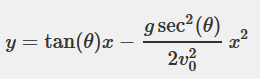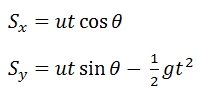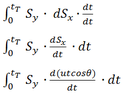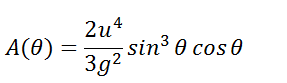- #1
Vedant97
- 2
- 0
I am trying to calculate the area under the curve of a projectile for a school project.
A simple way to do this is to integrate the following equation of the trajectory:
View attachment 3263
However I've tried to use another method. Since we have the two equations for the horizontal and vertical displacements (respectively):
View attachment 3264
View attachment 3265
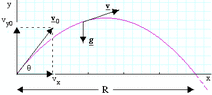
As it can be seen from the above graph, we can integrate Sy with respect to Sx to get the area under the curve. However since Sy and Sx themselves are in terms of 't' (other variables are considered constant), we multiply them by (dt/dt) which will give us:
View attachment 3266
(where Tt is the time when the projectile hits the ground)
Both methods ultimately simplify to give the equation:
View attachment 3267However, my teacher says that my method of multiplying the (dt/dt) is 'mathematically incorrect' even though both give the same results. But I believe that what I have done is correct. Can anyone help me come up with a justification as to why this is mathematically correct?
A simple way to do this is to integrate the following equation of the trajectory:
View attachment 3263
However I've tried to use another method. Since we have the two equations for the horizontal and vertical displacements (respectively):
View attachment 3264
View attachment 3265
As it can be seen from the above graph, we can integrate Sy with respect to Sx to get the area under the curve. However since Sy and Sx themselves are in terms of 't' (other variables are considered constant), we multiply them by (dt/dt) which will give us:
View attachment 3266
(where Tt is the time when the projectile hits the ground)
Both methods ultimately simplify to give the equation:
View attachment 3267However, my teacher says that my method of multiplying the (dt/dt) is 'mathematically incorrect' even though both give the same results. But I believe that what I have done is correct. Can anyone help me come up with a justification as to why this is mathematically correct?