issacnewton
- 1,035
- 37
Hi
Here is the statement of the problem from Ralph Grimaldi's discrete math book.
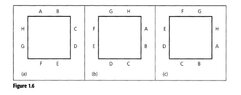
a) In how many ways can eight people, denoted A,B,...,H be seated about the square table shown in the figure (see attachment), where Figs 1.6 (a) and 1.6 (b) are considered the same but are distinct from Fig 1.6 (c).
I got this correct. The answer is \( 2(7!) \).
b)If two of the eight people , say A and B ,do not get along well, how many different seatings are possible with A and B not sitting next to each other ?
Here I reasoned as follows. I first calculate the no of seatings where A and B actually sit together. So with two of them fixed, six others can be permuted in \( 6! \) different ways. But seating arrangement of A , B is different that the arrangement B , A . So to account for this second arrangement we will nee to add \( 6! \) possible arrangements. So total seating arrangements for two of them together is \( 2(6!) \). So to get the answer for this part, we will need to subtract \( 2(6!) \) from \( 2(7!) \). So answer I am getting is 8640. But the answer given for this part is 7200. So can you find mistake in my reasoning ?
Thanks
(Malthe)
Here is the statement of the problem from Ralph Grimaldi's discrete math book.
a) In how many ways can eight people, denoted A,B,...,H be seated about the square table shown in the figure (see attachment), where Figs 1.6 (a) and 1.6 (b) are considered the same but are distinct from Fig 1.6 (c).
I got this correct. The answer is \( 2(7!) \).
b)If two of the eight people , say A and B ,do not get along well, how many different seatings are possible with A and B not sitting next to each other ?
Here I reasoned as follows. I first calculate the no of seatings where A and B actually sit together. So with two of them fixed, six others can be permuted in \( 6! \) different ways. But seating arrangement of A , B is different that the arrangement B , A . So to account for this second arrangement we will nee to add \( 6! \) possible arrangements. So total seating arrangements for two of them together is \( 2(6!) \). So to get the answer for this part, we will need to subtract \( 2(6!) \) from \( 2(7!) \). So answer I am getting is 8640. But the answer given for this part is 7200. So can you find mistake in my reasoning ?
Thanks
(Malthe)