Artificially discretized quantum states - is it a thing?

[Swamp Thing]

Here we have four electron detectors (e.g. electron multipliers) forming positively charged detection regions, with a negative back plate.

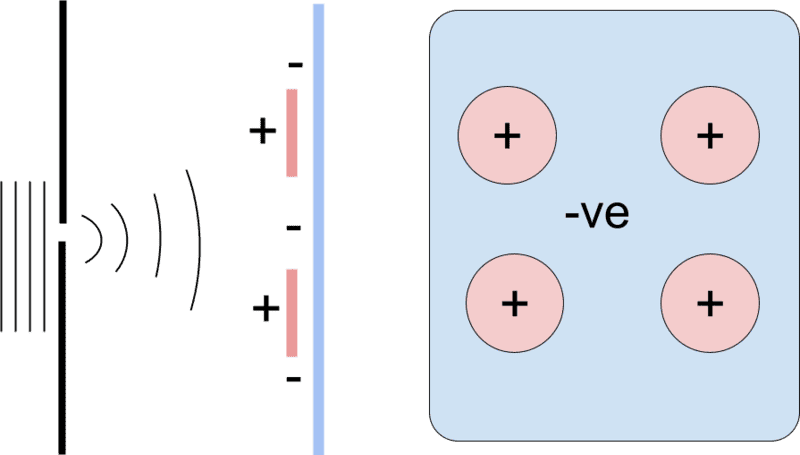
Mathematically, is it valid to describe this as a measurement with four eigenstates, considering that there are only four possible detection outcomes?

=== EDIT ===
Assume that the distance from first screen to detection plane is large enough (paraxial case?) that the phase variation over one detector is negligible.

 

[gentzen]

Mathematically, is it valid to describe this as a measurement with four eigenstates, considering that there are only four possible detection outcomes?

=== EDIT ===
Assume that the distance from first screen to detection plane is large enough (paraxial case?) that the phase variation over one detector is negligible.

If your measurements have only four diffent outcomes, then modeling that part as having four possible outcomes is valid. Your four outcomes seem to have excellent separation and very little crosstalk, so in your case it is additionally valid to model the measurement part as projection-valued measure, i.e. as a self-adjoint operator with 4 distict eigenvalues.

One possible interpretation of your question is whether it is valid to assume that the eigenspaces corresponding to those 4 distinct eigenvalues are one-dimensional. My feeling is that this is not valid, already for simple cases like the hydrogen atom. But I could be wrong, at least for the hydrogen atom.

Another interpretation of your question is whether the non-detection case would have had to be included in your possible outcomes, i.e. whether you should have used five possible outcomes for modeling the measurement part. But because of the positive and negavite charge situation that you stipulated, it is valid in your case to assume that it does not occur. Without that positive and negavite charge situation, you would have to either model it as a postselection situation (generally a good idea, in my opinion, even if the theory might be slightly unfamiliar), or have a fifth possible outcome with poor separation and significant crosstalk to the other cases, so that you must use positive operator-valued measure (POVM) instead of the simpler projection-valued measure modeling.