- #1
Math Amateur
Gold Member
MHB
- 3,998
- 48
I am reading Paul E. Bland's book, "Rings and Their Modules".
I am focused on Section 4.2: Noetherian and Artinian Modules and need some help to fully understand the proof of part of Proposition 4.2.4 ... ...
Proposition 4.2.4 reads as follows:

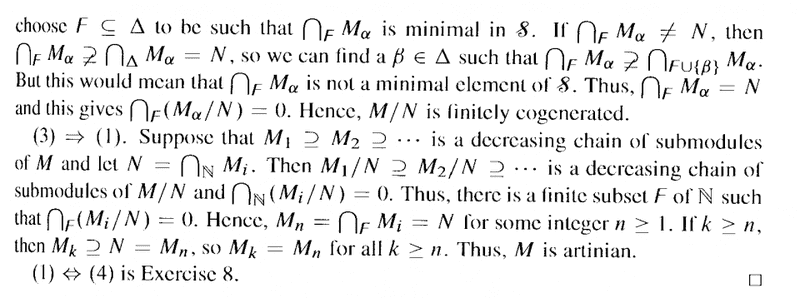
I need help to fully understand Part of the proof proving that ##(2) \Longrightarrow (3)## ...In that part of the proof Bland seems to be assuming that
## \bigcap_F M_\alpha = N ##
if and only if
## \bigcap_F (M_\alpha / N ) = 0 ##
In other words, if ##F = \{ 1, 2, 3 \}## then
##M_1 \cap M_2 \cap M_3##
if and only if
##M_1 / N \cap M_2 / N \cap M_3 / N## But why exactly is this the case ... ...
... ... how do we formally and rigorously demonstrate that this is true ...Hope someone can help ...
Peter
====================================================
Proposition 4.2.4 refers to the (possibly not well known) concept of cogeneration so I am providing Section 4.1 Generating as Cogenerating Classes ... ... as follows ...



I am focused on Section 4.2: Noetherian and Artinian Modules and need some help to fully understand the proof of part of Proposition 4.2.4 ... ...
Proposition 4.2.4 reads as follows:
I need help to fully understand Part of the proof proving that ##(2) \Longrightarrow (3)## ...In that part of the proof Bland seems to be assuming that
## \bigcap_F M_\alpha = N ##
if and only if
## \bigcap_F (M_\alpha / N ) = 0 ##
In other words, if ##F = \{ 1, 2, 3 \}## then
##M_1 \cap M_2 \cap M_3##
if and only if
##M_1 / N \cap M_2 / N \cap M_3 / N## But why exactly is this the case ... ...
... ... how do we formally and rigorously demonstrate that this is true ...Hope someone can help ...
Peter
====================================================
Proposition 4.2.4 refers to the (possibly not well known) concept of cogeneration so I am providing Section 4.1 Generating as Cogenerating Classes ... ... as follows ...
Attachments
-
 Bland - 1 - Proposition 4.2.4 - PART !.png71.2 KB · Views: 745
Bland - 1 - Proposition 4.2.4 - PART !.png71.2 KB · Views: 745 -
 Bland - 2 - Proposition 4.2.4 - PART 2.png31.1 KB · Views: 689
Bland - 2 - Proposition 4.2.4 - PART 2.png31.1 KB · Views: 689 -
 Bland -1 - Section 4.1 - PART 1.png36.1 KB · Views: 689
Bland -1 - Section 4.1 - PART 1.png36.1 KB · Views: 689 -
 Bland - 2 - Section 4.1 - PART 2.png43.2 KB · Views: 714
Bland - 2 - Section 4.1 - PART 2.png43.2 KB · Views: 714 -
 Bland - 3 - Section 4.1 - PART 3.png45.4 KB · Views: 722
Bland - 3 - Section 4.1 - PART 3.png45.4 KB · Views: 722