Monoxdifly
MHB
- 288
- 0

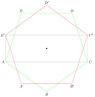
In the icosahedron above, what is the proper way of determining the length of PP'?
My workmate thinks that it is twice the length of P to the midpoint of E'C' plus E'A, since she thinks that (and it does look) ACC'E' is a rectangle.
However, I think that E'A must not be the height of the rectangle, since the height of the rectangle should be the height of the triangle A'BB'. Also, I think the icosahedron's height is twice the length of P to the center of A'B'C'D'E' plus triangle A'BB', though I am not sure if the length of P to the center of A'B'C'D'E' equals the length of P to the midpoint of E'C'.
Which one of us is correct?