Assumptions for string vibrator system

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

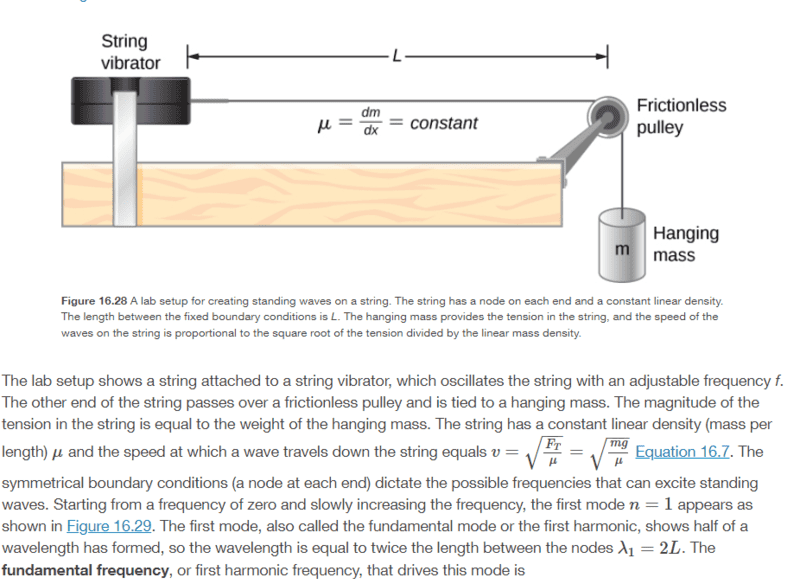
Is it possible to calculate the time it takes for the initial antinode at the string vibrator to become a node in the transient phase of the system? Also do we assume that once the system has reached steady state, that the mass has such a large inertia that it is stationary so acts as a fixed boundary reflecting the waves at a 180-degree phase shift relative to the incident traveling waves?

Many thanks!

 

[haruspex]

Is it possible to calculate the time it takes for the initial antinode at the string vibrator to become a node in the transient phase of the system? Also do we assume that once the system has reached steady state, that the mass has such a large inertia that it is stationary so acts as a fixed boundary reflecting the waves at a 180-degree phase shift relative to the incident traveling waves?

Many thanks!

Not sure I understand your first question. The frequency is increased slowly, meaning that when arriving at any given frequency the transient phase to steady state is negligible.
Yes, the movement of the mass is also considered negligible here.

 

[BvU]

Hi,

Is it possible to calculate the time it takes for the initial antinode at the string vibrator to become a node in the transient phase of the system?

That point is as good as fixed. Check with fig 16.29

Also do we assume that once the system has reached steady state, that the mass has such a large inertia that it is stationary so acts as a fixed boundary reflecting the waves at a 180-degree phase shift relative to the incident traveling waves?

The fixed point is at the pulley.

 

[nasu]

How would you have a node at the vibrator end? And where is figure 29? Does it show a node at the vibrator end?

 

[berkeman]

How would you have a node at the vibrator end?

Yeah, I don't get that either. How do you drive vibrations on a string from a node?

 

[BvU]

This is practical physics. The string resonates and the deviations from equilibrium at antinodes are much greater than at the vibrator end, so fapp (for all practical purposes) that end is a node. (Thorough experimentation can reveal how near the virtual node is further to the left).



$\$

 

[berkeman]

The string resonates and the deviations from equilibrium at antinodes are much greater than at the vibrator end, so fapp (for all practical purposes) that end is a node. (Thorough experimentation can reveal how near the virtual node is further to the left).

Huh, TIL. Thanks @BvU

 

[BvU]

Does it show a node at the vibrator end?

Calling my bluff eh ?
My reputation is in the hands of @ChiralSuperfields

$\$

 

[nasu]

I asked this before you posted your video. This is better than figure 29, whatever that is.

 

[nasu]

I have played several times with this PHET simulation but I have not relized (until now) that by using a small amplitude of one end you can produce a much higher amplitude at the node.
So, it works even for a simulation, not just in the real world.

 

[haruspex]

I have played several times with this PHET simulation but I have not relized (until now) that by using a small amplitude of one end you can produce a much higher amplitude at the node.
So, it works even for a simulation, not just in the real world.

I note that in some cases there is a real node just to the right, in others a virtual node just to the left. It would be interesting to predict that displacement as a function of the parameters.

 

[member 731016]

Thank you @haruspex, @BvU, @nasu, and @berkeman for your replies!

Sorry for not posting earlier. Here is the figure requested.

For reference, here is the textbook which it was from. https://openstax.org/books/university-physics-volume-1/pages/16-6-standing-waves-and-resonance

Many thanks!