Attempt at volume integration to compute the full field equation

[tade]

I'm trying to figure out this volume integral, a triple integral, of a 9-variable function.

3 Cartesian-dimension variables, and 6 primed and un-primed co-ordinates.

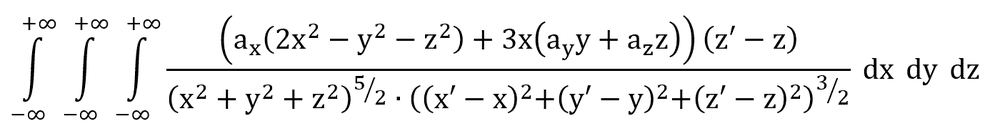
After the volume integration, the un-primed co-ordinates will have been gotten rid of, leaving a field function in terms of the primed co-ordinates.

It's looks really tricky to my simple mind, I hope I can get some pointers, or recommendations on software which could potentially help solve it.

 

[tade]

maybe Maple might be of help?

 

[phyzguy]

In the homework section, you are supposed to show us some effort of things you have tried. How have you approached the problem?

 

[tade]

In the homework section, you are supposed to show us some effort of things you have tried. How have you approached the problem?

sorry, I'm not sure how to begin, was hoping for some pointers

 

[phyzguy]

Try converting to spherical polar coordinates with the z-axis pointing along r'. Then the denominator becomes:
$$r^5 (r^2 + r'^2 - 2r r' \cos(\theta))^{3/2}$$

 

[Ray Vickson]

Try converting to spherical polar coordinates with the z-axis pointing along r'. Then the denominator becomes:
$$r^5 (r^2 + r'^2 - 2r r' \cos(\theta))^3$$

The "dimensions" of the second factor in the (original) denominator are $r^3$, so the second factor in the new denominator must be $(r^2 + r'^2 - 2 r r' \cos \theta)^{3/2}.$

 

[phyzguy]

The "dimensions" of the second factor in the (original) denominator are $r^3$, so the second factor in the new denominator must be $(r^2 + r'^2 - 2 r r' \cos \theta)^{3/2}.$

Thanks. I corrected my post.

 

[tade]

Try converting to spherical polar coordinates with the z-axis pointing along r'. Then the denominator becomes:
$$r^5 (r^2 + r'^2 - 2r r' \cos(\theta))^{3/2}$$

oh, then that would turn r' into a scalar variable right?

The scalar variable being the length of r', the magnitude of the vector

 

[phyzguy]

The scalar variable being the length of r', the magnitude of the vector

Yes, but r' is a constant with respect to the integration. It is not a variable being integrated over.

 

[tade]

Yes, but r' is a constant with respect to the integration. It is not a variable being integrated over.

ok, I guess you could say the integral is sort of like ∂x∂y∂z? or ∂r∂θ∂Φ

 

[phyzguy]

ok, I guess you could say the integral is sort of like ∂x∂y∂z?

I don't know what you are asking. Can you re-write the integral with the change of variables I suggested?

 

[tade]

I don't know what you are asking. Can you re-write the integral with the change of variables I suggested?

ok, I guess you could say the integral is sort of like ∂x∂y∂z? or ∂r∂θ∂Φ

what I meant was instead of being 'd', it is effectively '∂'

Also, do you think I should modify the three 'a' variables, or leave them as they are?

 

[phyzguy]

what I meant was instead of being 'd', it is effectively '∂'
Also, do you think I should modify the three 'a' variables, or leave them as they are?

Well, since x,y,z are independent variables, when you integrate over x, for example, you treat y and z as constant. But this is always the case in multi-dimensional integration, and one typically uses the notation dx instead of $\partial x$. As for the a's, I am assuming they are constants (not functions of x,y,z). If you know otherwise, you will have to include their functional form in the integration.

 

[tade]

Well, since x,y,z are independent variables, when you integrate over x, for example, you treat y and z as constant. But this is always the case in multi-dimensional integration, and one typically uses the notation dx instead of $\partial x$. As for the a's, I am assuming they are constants (not functions of x,y,z). If you know otherwise, you will have to include their functional form in the integration.

The a's are components of the vector a. But a is just a single vector, it doesn't represent 3-D space.

 

[phyzguy]

The a's are components of the vector a. But a is just a single vector, it doesn't represent 3-D space.

Is it a constant vector, or is it a function of (x,y,z)? that's the question you need to know the answer to.

 

[tade]

Is it a constant vector, or is it a function of (x,y,z)? that's the question you need to know the answer to.

A constant vector, independent of (x,y,z)

 

[tade]

Is it a constant vector, or is it a function of (x,y,z)? that's the question you need to know the answer to.

@Ray Vickson @phyzguy I tried integrating with an unmodified 'a' in Maple, unfortunately it couldn't solve it.

I hope I can find the solution.

In fact, I actually have what might be a potential solution. I just want to prove that it is in fact the solution.

$$\frac{{a_z}x}{(x^2+y^2+z^2)^\frac{3}{2}}$$
$a_x$ and $a_y$ are no longer in the equation.

This is in terms of the primed co-ordinates, though I didn't include the prime marks.x' is related to r' by means of two angles. Since the numerator is x', this means that the triple integral introduces two new angular variables to make up for the reduction of two variables in the earlier simplification, though I'm not sure how that might happen.

 

[tade]

@Ray Vickson @phyzguyIn fact, I actually have what might be a potential solution. I just want to prove that it is in fact the solution.

$$\frac{{a_z}x}{(x^2+y^2+z^2)^\frac{3}{2}}$$
$a_x$ and $a_y$ are no longer in the equation.

This is in terms of the primed co-ordinates, though I didn't include the prime marks.x' is related to r' by means of two angles. Since the numerator is x', this means that the triple integral introduces two new angular variables to make up for the reduction of two variables in the earlier simplification, though I'm not sure how that might happen.

@phyzguy, I've realized that in order to convert the un-primed x,y,z co-ordinates to something in terms of r, I'll need to convert them to intermediate Cartesian co-ordinates, which adds the two new angular variables, using the rotation matrix. But just 2 out of the 3 angles of 3-D rotation.

I'll then have to apply the spherical co-ordinate transformations, adding another two angular variables.

Also, any suggestions on proving or disproving my possible solution?

 

[phyzguy]

@phyzguy, I've realized that in order to convert the un-primed x,y,z co-ordinates to something in terms of r, I'll need to convert them to intermediate Cartesian co-ordinates, which adds the two new angular variables, using the rotation matrix. But just 2 out of the 3 angles of 3-D rotation.

I'll then have to apply the spherical co-ordinate transformations, adding another two angular variables.

Also, any suggestions on proving or disproving my possible solution?

Two comments:
(1) I don't know what you mean by "intermediate Cartesian co-ordinates". You are integrating over all space, so you are free to use any set of coordinates that you want. Just transform from (x,y,z) to (r,θ,φ) and go from there.

(2) I do not think that your proposed solution is correct.

 

[tade]

(1) I don't know what you mean by "intermediate Cartesian co-ordinates". You are integrating over all space, so you are free to use any set of coordinates that you want. Just transform from (x,y,z) to (r,θ,φ) and go from there.

For example, $x=x_r cosA - y_r sinA$ and $x_r = r sinθ ⋅cosφ$

Thus adding a new angular variable A.

(2) I do not think that your proposed solution is correct.

sorry, what's the reasoning?

 

[phyzguy]

For example, $x=x_r cosA - y_r sinA$ and $x_r = r sinθ ⋅cosφ$
Thus adding a new angular variable A.

Why not just $x = r \sin(\theta) \cos(\phi); y = r \sin(\theta) \sin(\phi); z = r \cos(\theta)$

sorry, what's the reasoning?

What is your reasoning for thinking it is the solution?

 

[tade]

Why not just $x = r \sin(\theta) \cos(\phi); y = r \sin(\theta) \sin(\phi); z = r \cos(\theta)$

The original unprimed co-odn.s are in co-odn. system where r' isn't always pointing in the z-direction.

In 2-D, we've got one angle of rotation, in 3-D, three angles, but the direction of a vector needs only two angles to be specified.

What is your reasoning for thinking it is the solution?

It has to do with the moving magnet and conductor problem.

A static magnetic field B in the magnet's frame is transformed into a varying magnetic field B' in the conductor's frame by means of a Galilean velocity boost, v.
There is a magnetically induced electric field E' in the conductor's frame.

It can be shown that $∇×E'=-\frac{∂B'}{∂t'}=∇×(v×B)$

It is then inferred that $E'=v×B$. I'm trying to prove that that is indeed the case.

B is of a current element following the Biot-Savart law. The volume integral is to obtain E', and it uses a form similar to the Biot-Savart Law.

$∇⋅(\frac{∂B'}{∂t'})=\frac{∂}{∂t'}(∇⋅B')=\frac{∂}{∂t'}(∇⋅B)=0$, so this calculation of the E-field will satisfy $∇×E'=-\frac{∂B'}{∂t'}$.

 

[phyzguy]

As I've tried to point out, you are integrating over all space. So you are free to use whatever coordinate system you choose. That means you can choose a coordinate system where the z-axis is aligned along r'. But you don't seem to accept this, so go ahead and solve the problem with whatever means you are comfortable with.

 

[tade]

As I've tried to point out, you are integrating over all space. So you are free to use whatever coordinate system you choose. That means you can choose a coordinate system where the z-axis is aligned along r'. But you don't seem to accept this, so go ahead and solve the problem with whatever means you are comfortable with.

huh? I accept it.

Just that we might need to use the 3-D rotation matrices, adding another two angular variables.

And if proving is easier than integrating, I'll take it.

 

[phyzguy]

huh? I accept it.

Just that we might need to use the 3-D rotation matrices, adding another two angular variables.

And if proving is easier than integrating, I'll take it.

You don't need any rotation matrices. Just choose a new set of variables - (r, θ,φ), with the z-axis pointing along r'.

 

[tade]

You don't need any rotation matrices. Just choose a new set of variables - (r, θ,φ), with the z-axis pointing along r'.

Does that imply that my possible solution is incorrect, since it can't be expressed solely in terms of r' and the a's?

And we're integrating over a 3-D field, I was thinking, when we rotate r' into alignment with the z-axis, the 3-D field rotates as well.

 

[phyzguy]

A better way to think of it is that you are leaving the r' vector unchanged, but using a different set of (x,y,z) variables to do the integration.

 

[tade]

A better way to think of it is that you are leaving the r' vector unchanged, but using a different set of (x,y,z) variables to do the integration.

hmm, but that seems like a case of relative motion; the vector unchanged and the co-ordinate system rotating, or the vector rotating and the co-ordinate system unchanged. The mathematical result should be the same.